左メニューなどが狭く見づらくなった場合には、ウィンドウ幅を調節してみて下さい。
 Webページでは数式を表すためにLaTeX表記が使えるMathJaxを利用します。
WebブラウザにはSafari/Chrome/Firefoxを使って下さい。
Webページでは数式を表すためにLaTeX表記が使えるMathJaxを利用します。
WebブラウザにはSafari/Chrome/Firefoxを使って下さい。
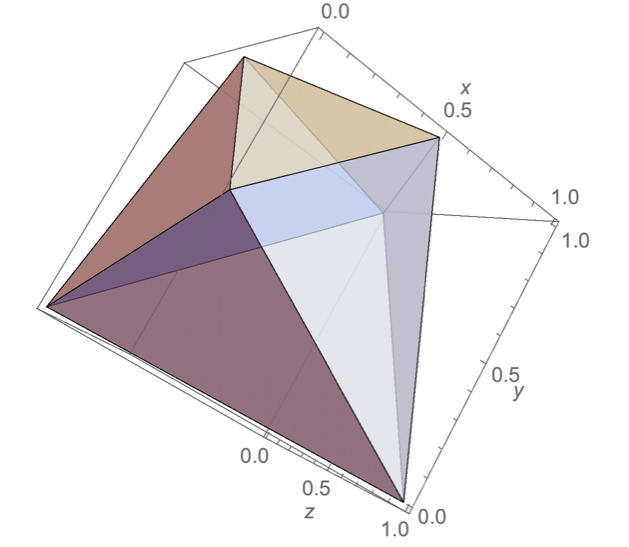
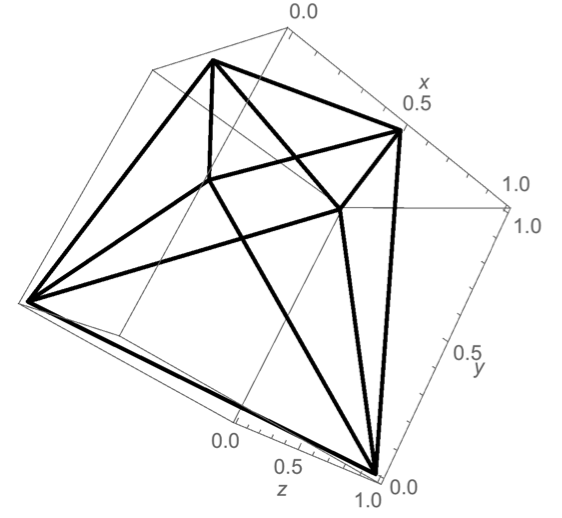
極小凸イマジナリーキューブの例
 参考:イマジナリーキューブ・パズル(立木秀樹/京都大学大学院)
参考:イマジナリーキューブ・パズル(立木秀樹/京都大学大学院) Imaginary Cube (立木秀樹)
Imaginary Cube (立木秀樹)
極小凸イマジナリーキューブ
「イマジナリーキューブ・パズル」にある以下の考察は極小凸イマジナリーキューブの本質を理解する上で初等的であるが興味深い。
ある凸立体$P$がイマジナリーキューブであるための必要十分条件は、立方体の全ての辺上に$P$の頂点があることである。 必要性はただちに明かで、そのように$P$の頂点が配置されていないと直交する3方向からみたとき、正方形には見えない。 特に$P$が極小凸イマジナリーキューブであるの時、$P$は立方体と$P$ との共通部分 $\text{立方体}\cap P$ の凸包(convex hull)になっていて、よって$P$ は全ての頂点は立方体の辺上にある多面体となる。
$P$の頂点のうち、 立方体の頂点であるものを頂-頂点といい、この集合を$V(P)$と表す。 また、立方体の頂点ではないものを辺-頂点と言おう。 もし、立方体のある辺上に頂点があり、さらにもう一つの頂点がその辺の両端(頂点-頂点)以外に頂点があれば、それを取り除いてより小さな凸イマジナリーキューブを作ることかできる。 何故なら、その辺に平行か方向から見たとき、辺上の頂点の一つを取り除いても見え方は変化しないからである。 一方で、立方体の辺の両端に頂点がある時は、両方の頂点共に他の辺の唯一の頂点となっていることがあり得るため、それらの頂点を取り除けない場合が生じる。
このことから、極小凸イマジナリーキューブ$P$の頂点は、
- 各辺上に辺-頂点が1個だけある
- 頂-頂点が1個ある
- 頂-頂点が2個ある
立方体のある頂点 $a$ とその隣の3頂点が全て頂-頂点集合 $V(P)$ に属すれば、このとき $a$ を除いても凸イマジナリーキューブとなるので、$V(P)$ はそのような部分集合を含まない。 逆に、この条件を満たすような立方体の頂点集合 $S$ に対し、$S$の要素として端点が含まれない辺上に辺-頂点を1つづつ選べば極小凸イマジナリーキューブ$P$が得られる。
2つの極小イマジナリーキューブ$P$と$P'$について、$V(P) = V(P′)$である時、$P$ と $P′$ は同値だと定義する。 すると、同値類は上記の条件を満たす立方体の頂点集合と対応して存在し、それは、回転で重なるものを同一視するとみなすと、16種類、鏡像も同一視すれば15種類あることがわかる。 よって、立方体の極小凸イマジナリーキューブは 16種類(鏡像を同一視すれば15種類に分類される。
16個の全極小イマジナリーキューブ
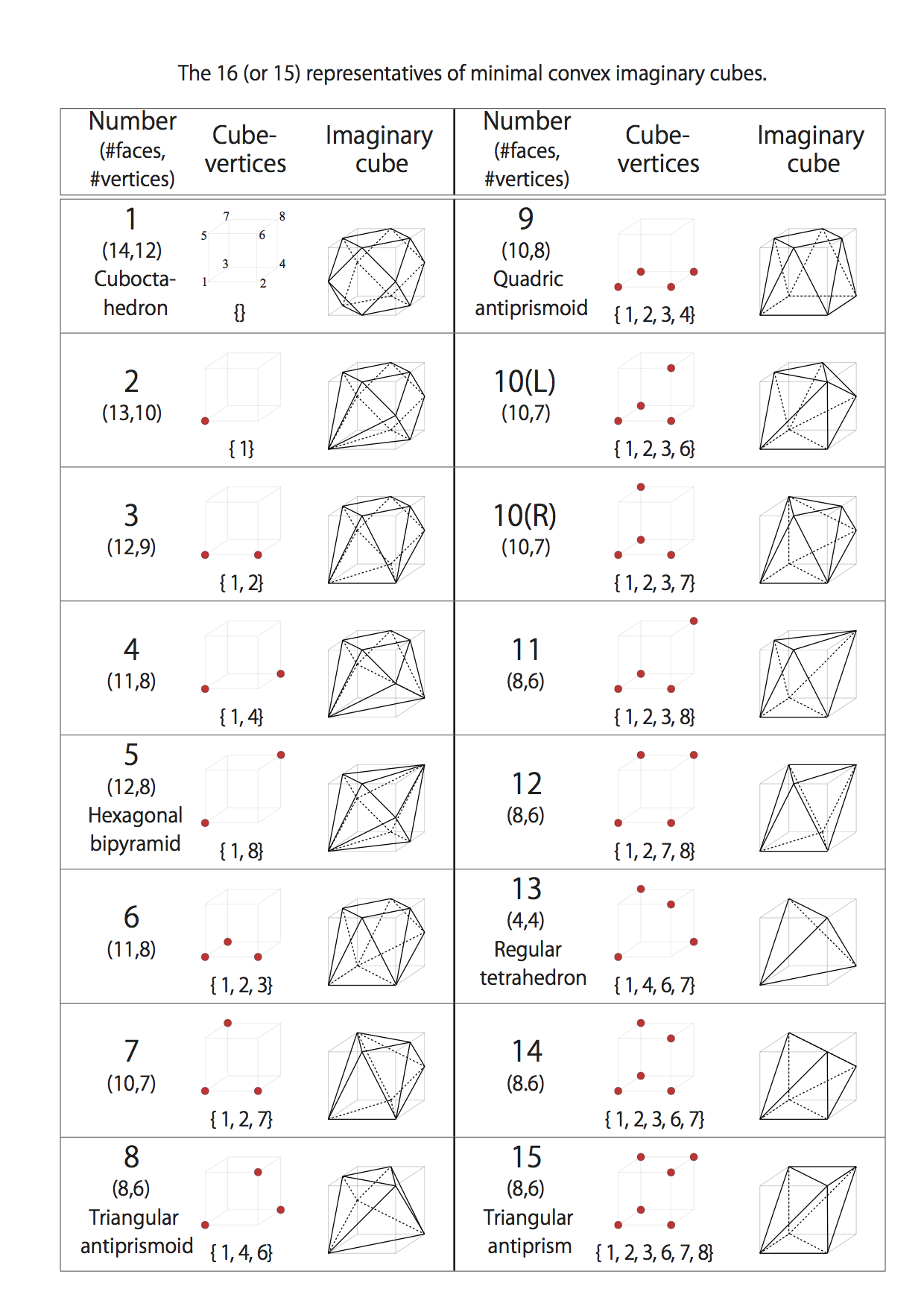 クリックしてで拡大
クリックしてで拡大from イマジナリーキューブ・パズル(図4: 16種類の極小凸イマジナリーキューフ: 立木秀樹/京都大学大学院より)
幾つかのイマジナリーキューブ
立方体の頂点以外にあるイマジナリーキューブの頂点は立方体の辺に中点にある。 格別の興味深いのは、重六角錐 H と反三角錐台 T である。
 正四面体(tetrahedron)
正四面体(tetrahedron)-
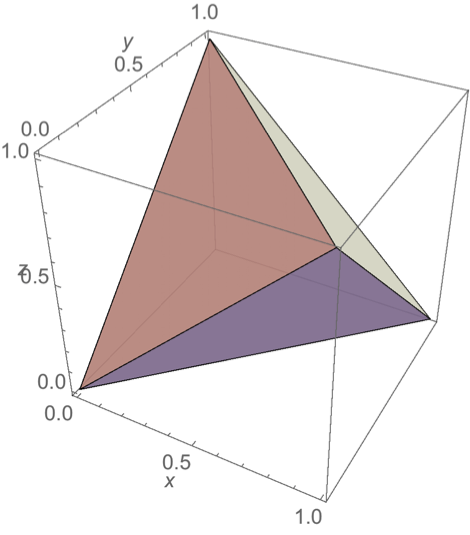
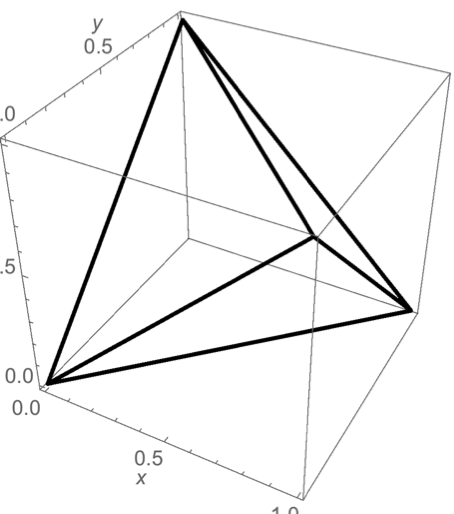
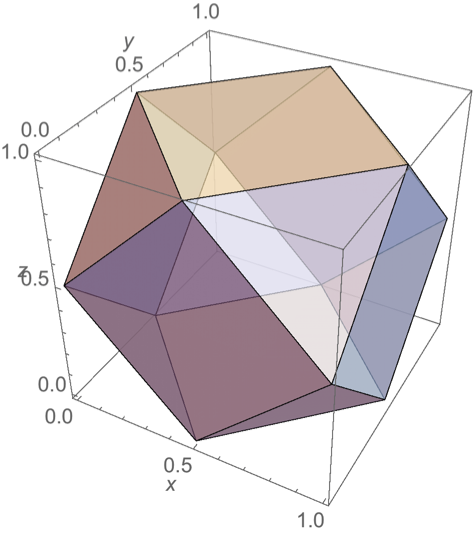
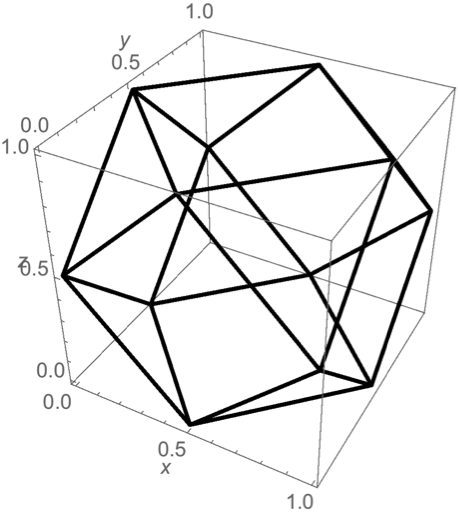
 立法八面体(cuboctahedron)
立法八面体(cuboctahedron)-
 重六角錐(hexagonal bipyramid): H
重六角錐(hexagonal bipyramid): H-
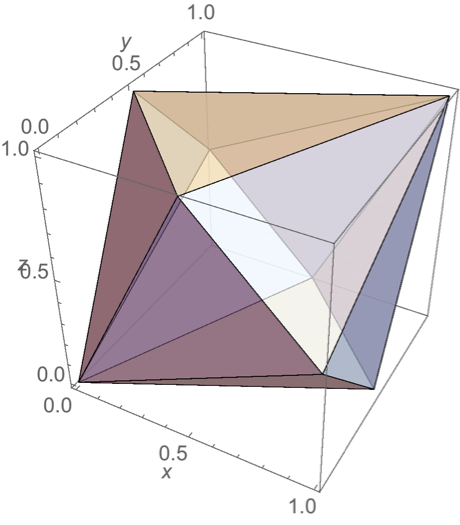

 反三角錐台(triangular antiprismoid): T
反三角錐台(triangular antiprismoid): T-