左メニューなどが狭く見づらくなった場合には､ウィンドウ幅を調節してみて下さい。

Webページでは数式を表すためにLaTeX表記が使えるMathJaxを利用します。 WebブラウザにはSafari/Chrome/Firefoxを使って下さい。

課題：イマジナリーキューブの制作

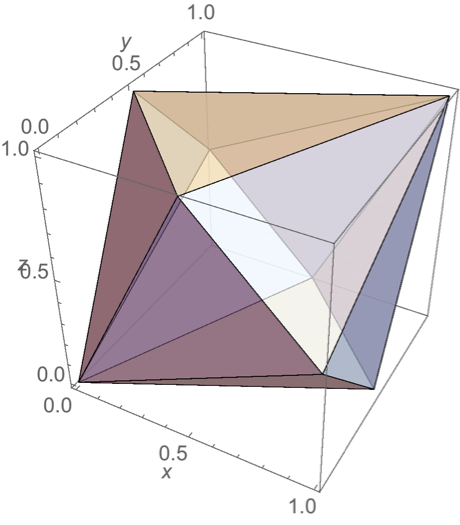
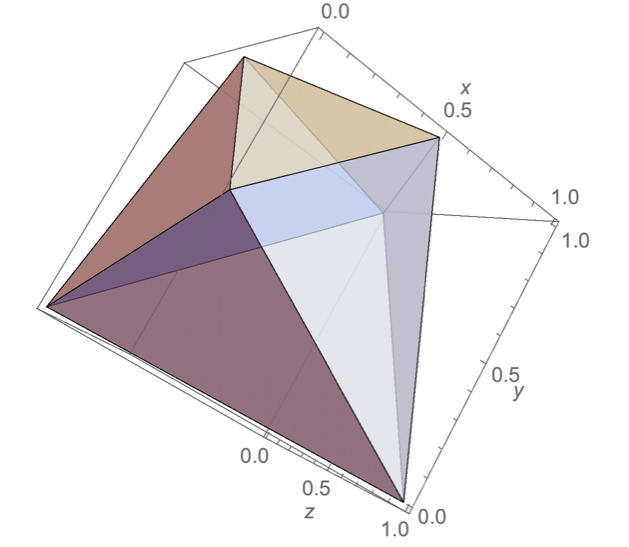
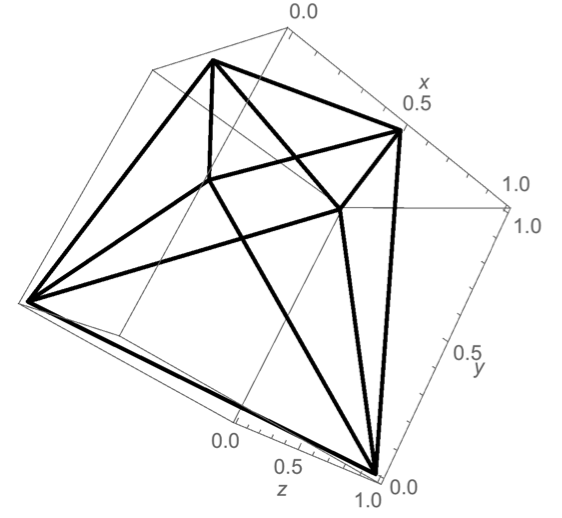
「イマジナリーキューブ・パズル」にある以下の考察は極小凸イマジナリーキューブの本質を理解する上で初等的であるが興味深い。

ある凸立体$P$がイマジナリーキューブであるための必要十分条件は、立方体の全ての辺上に$P$の頂点があることである。 必要性はただちに明かで、そのように$P$の頂点が配置されていないと直交する3方向からみたとき、正方形には見えない。 特に$P$が極小凸イマジナリーキューブであるの時、$P$は立方体と$P$ との共通部分 $\text{立方体}\cap P$ の凸包(convex hull)になっていて、よって$P$ は全ての頂点は立方体の辺上にある多面体となる。

作成するイマジナリーキューブ達

立方体の頂点以外にあるイマジナリーキューブの頂点は立方体の辺に中点にある。 重六角錐(H)を3個と反三角錐台(T) 6個を、たとえば以下の要領で作成する。

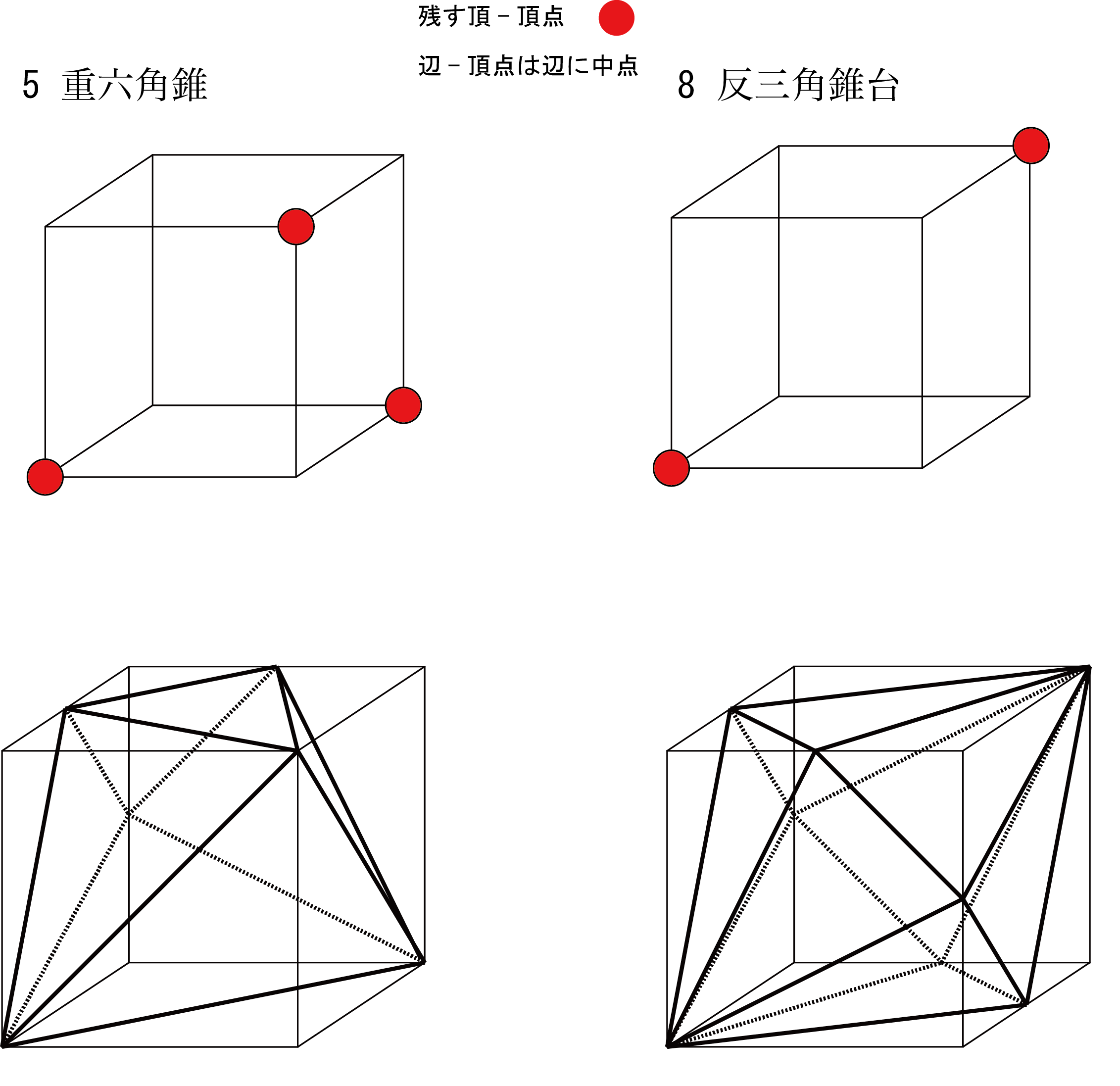ヒント：
[展開図] 極小凸Imaginary cube とそれを用いた教材(Hideki Tsuiki)の5番(H)と8番(T)から 作成したイマジナリーキューブは1辺5cmの立方体内に正確に収まる。
重六角錐(hexagonal bipyramid): H
反三角錐台(triangular antiprismoid): T

制作課題

[重要注意]

大きさ2の立方体に、長さ8cm幅4cmのラベルに以下の4行を太く大きく明記(鉛筆不可)
  1. 学部と学科
  2. 学年
  3. 学生番号
  4. 氏名
この条件を全て満たさない提出は評価しない。
正確な美しい立体作成が必須です。 たとえば、大きさ1=5cm, 大きさ2=10cmとする。
  1. イマジナリーキューブを格納する大きさ1の透明な立方体の箱を作成する。
  2. イマジナリーキューブ Hを3つ、Tを6つの合計9個を制作する。 自分で彩色してみると楽しいよ。
  3. 大きさ1の透明な立方体にHとTがぴたりと収まることを確認する。
  4. 大きさ2の透明な立方体の箱を作成し、3つのHと6つのTをぴたりと詰め込む。

市販のイマジナリーキューブ・パズルの様子

クリックしてで拡大
大きさ1の立方体も付いてくる。大きさ2のアクリル立方体にはめ込まれていた6つのT（白）と3つのH（茶）。 京都大学総合博物館ショップ・ミュゼップで工芸品として説明書付きで発売中。
詳しくは イマジナリーキューブ パズル 3H=6T