単頂点平坦折り

平坦折り(flat fold)

平坦折りとは、山折り(moutain crease)と谷折り(vallay crease)の折れ目に沿って紙が平らに折れるようなOrigamiである。

平坦折りでは、紙の厚さが無限小(zero)と見なすときは共に同じ平面を共有する(coplain)ように折られるが、紙が有限の厚さがある場合の「平坦折り」は別種の考察が必要になる。

単頂点折り

単頂点折り(single vertex folding)とは、1枚の紙にである直線が唯一つの交点（頂点）となような折りの展開図である。

ある頂点に集まる山折りおよび谷折りの折れ目線の数を頂点の次数(degree)という。

単頂点平坦折り

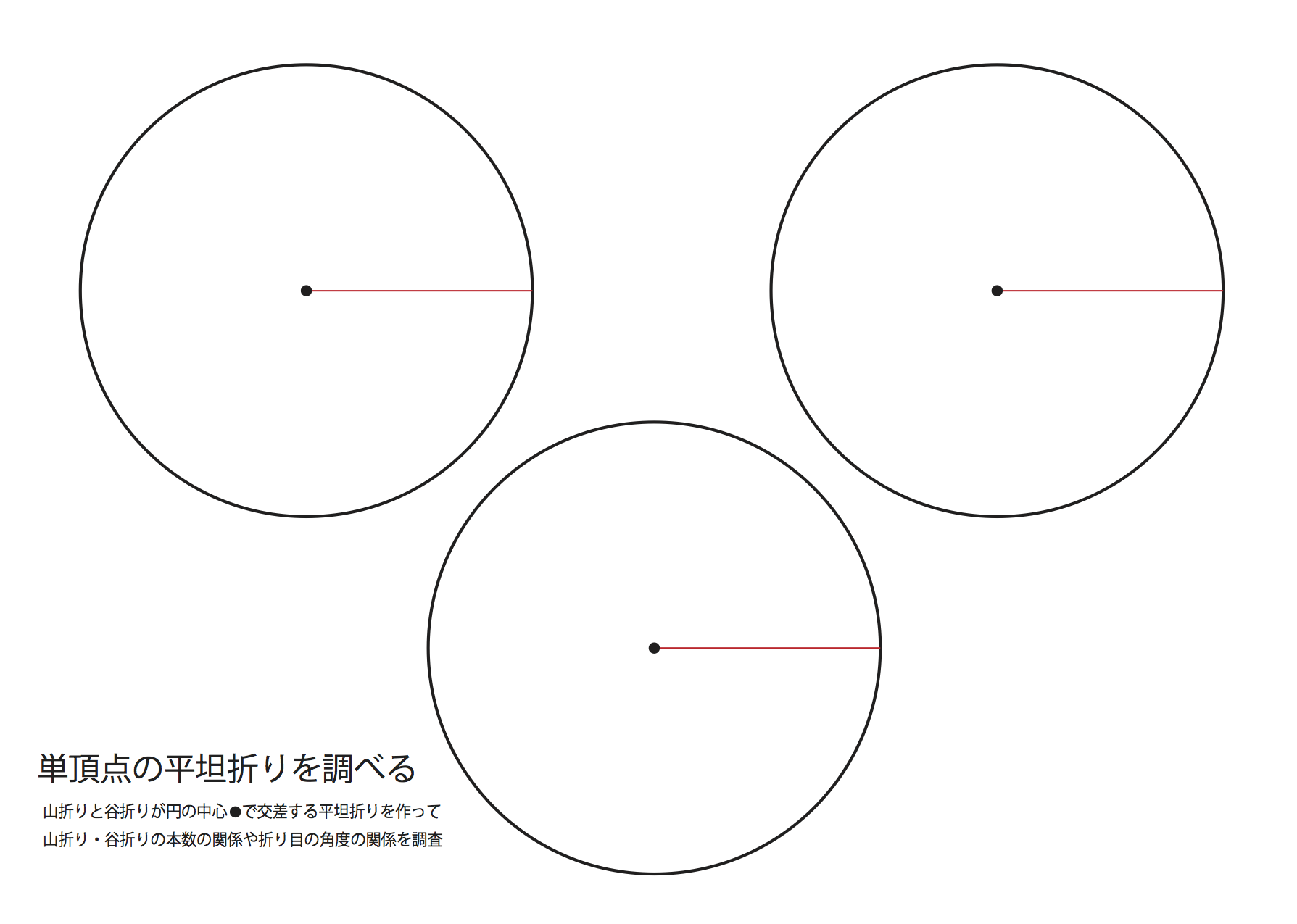単頂点平坦折りは円の中心を単頂点とする半径1の円板を、中心から延びる山および谷折りに沿って、下の図のように平坦に折り潰すことで調べることができる。

単頂点の平坦折りを調べる(A4印刷用)

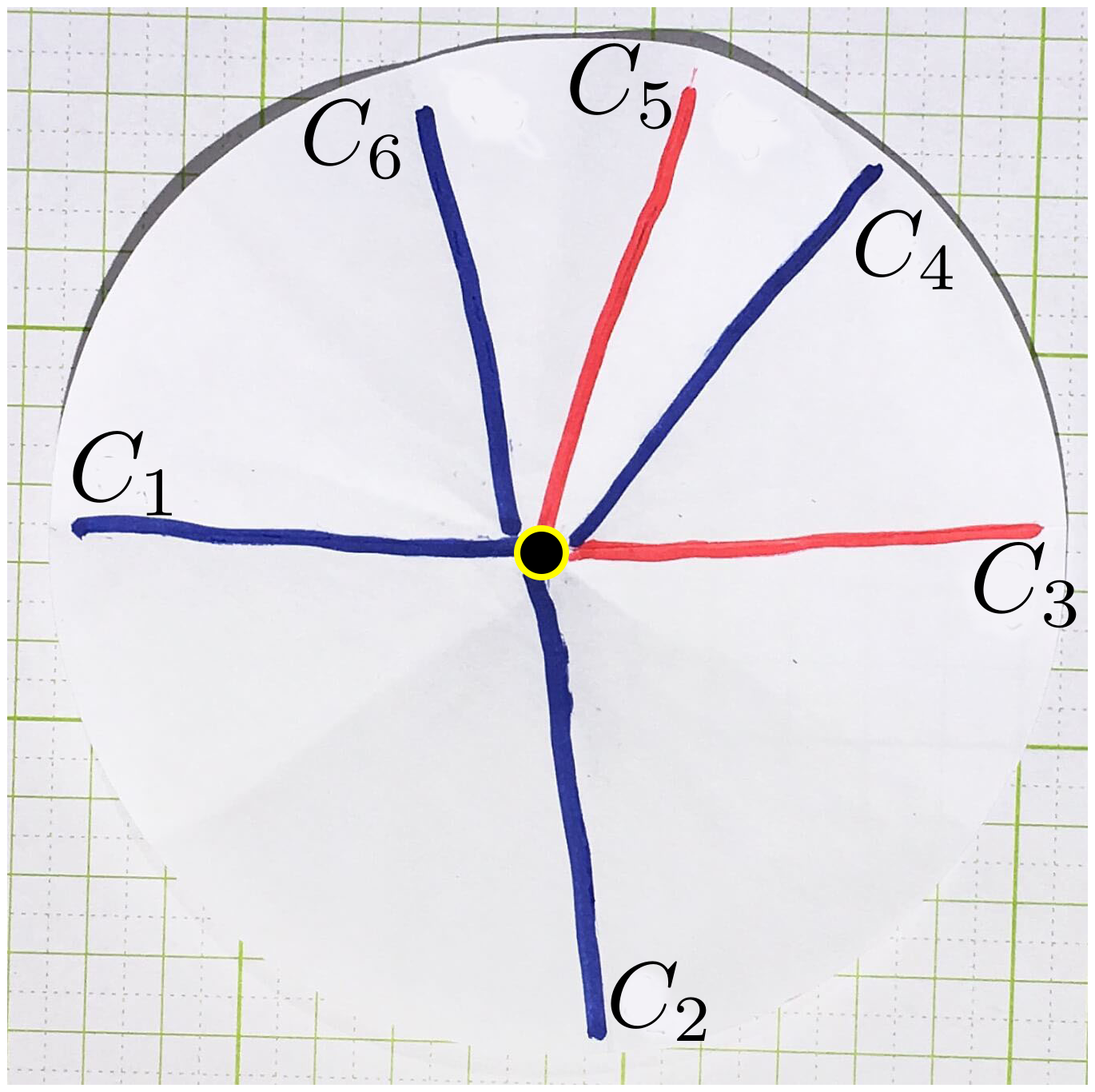
次の4図は、単頂点を通る折れ目$C_1, C_2, C_3, C_4, C_5, C_6$を左端図のような山折り(赤線)と谷折り(青線)の関係で平坦下折りした様子を表している。

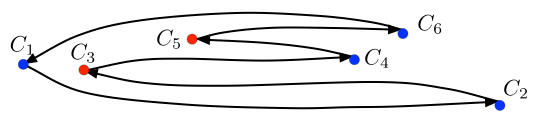
単調点平坦折りは、円板を平坦折りして横からその周囲を眺めてるようにみればその様子が記述できる。最右端の図のように、平坦折りされた円周は折れ目 $C_1, C_2, C_3, C_4, C_5, C_6$をつなぐ閉曲線となっている（図では同一平面にないように開いて描いてある）。

図のように折れ込むと平坦折りが達成されるのあるが、一般に平坦折りによって紙がどのように重なり合うかは折り目だけでは定めることができない（正しい単頂点平坦折りでも、その折り方は複数あり得る）。

演習：正しく平坦に折れ畳むことができ、しかもその折り方が複数あるような単頂点平坦折りとなる山折りと谷折りを単位円板に書き込んで、実際に平坦折りしてその様子を示しなさい。

単調点平坦折りの必要条件

定理（Pre 前川-Justin）:
平坦折りの頂点から延びている山折りの本数$M$と谷折りの本数$V$は \[ M= V+2\qquad \text{or}\qquad V=M+2 \] のどちらかの関係にある。

系:
単頂点平坦折りの頂点の次数は常に偶数である。

定義（局所最小角）:
頂点から延びる折れ目と頂点中心とする円板で切り取られる領域は扇形(fan shape)$f_1,f_2,f_3,\dots$をなしている。連続した3つの隣接する扇形$f_{k-1},f_k, f_{k+1}$において、中央の扇形の角度$a_k$がそれに隣接する左右の角度$a_{k-1}, a_{k+1}$よりも小さいとき（$a_k < a_{k-1}, a_{k+1}$）、角を局所最小角という。

局所最小定理:
任意の平坦折りにおいて、勅書的に最小な角を持つ扇形は、山折りと谷折りで区切られていなければならない。

Pre 前川-Justin定理、その系である偶数次数定理、および>局所最小定理はどれも平坦折りであるための必要定理であり、これらのどの2つを満たしているだけでは平坦折りであるために十分な条件を与えない。

演習：単頂点折りにおいて、平坦折りになり得ない次数4および次数6の折り目パターンの例を作りなさい。このとき、山折りの本数$M$と谷折りの本数$V$および局所最小角がどうなっているかを報告しなさい。

演習：上の単頂点折りが平坦折りになり得ない例に対して、それらを平坦折りとするために山折りまたは谷折りをどのように降らせば良いかの例を与えなさい。このとき、頂点の次数、山折りの本数$M$と谷折りの本数$V$および局所最小角がどうなっているかを報告しなさい。

単頂点平坦折りの必要十分条件

頂点の周りに$n$個の扇形 $f_1, f_2, f_3,\dots, f_n$ が集まっているとする。それらの扇形の角度を$\theta_1, \theta_2,\theta_3, \dots, \theta_n$ とすると、明らかに次のようなっている。 \[ \theta_1 + \theta_2 + \theta_3 + \dots + \theta_n=360 \]

前川-Justinの定理:
偶数次数を持つ頂点が平坦折りであるための必要十分条件は扇型の角度 $\theta_1, \theta_2,\theta_3, \dots, \theta_n$ の交代和がゼロ \[ \sum_{k=1}^{n-1}\theta_k-\theta_{k+1}=(\theta_1 - \theta_2) + (\theta_3 - \theta_4) +\dots =0 \] つまり、 \[ \theta_1+\theta_3+\theta_5 +\dots= \theta_2+\theta_4+\theta_6+\dots \]

必要性の証明はたやすいが、十分性については簡単ではない。

ただし、この定理は平坦折りができる山折りと谷折りの割り当てが存在することを保証するものであって（山折りの本数$M$と谷折りの本数$V$は$M+V=n$で、$M=V+2$または$V=M+2$の関係にある）、それらの具体的割り当ての仕方を構成するわけではない。

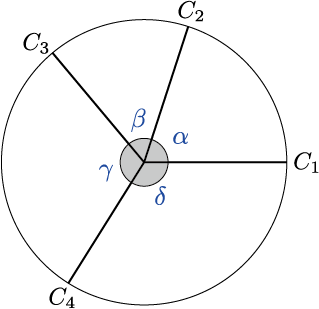特に次数4の頂点において、証明は容易である。左図のように4つの扇形の角度を $\alpha, \beta, \gamma, \delta$ とする。このとき \[ \alpha+\gamma=\beta+\delta=\pi. \]

演習：単頂点折りでPre前川-Justinの定理および局所最小定理をみたし、また前川-Justinの定理を満たすような扇形の角度を持つような次数6及び次数8の単頂点平坦折りの例を作って見せなさい。

挑戦してみよう

正方形の地図をその一辺が3分の1になるように次の折れ目を付けた。この地図は平坦に折れるだろうか？

地図折りパズル(A4用紙)