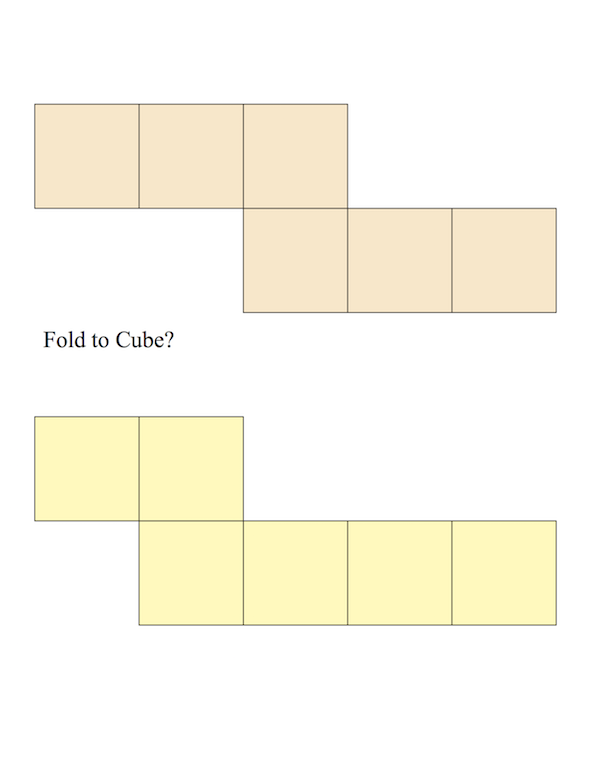
左メニューなどが狭く見づらくなった場合には、ウィンドウ幅を調節してみて下さい。
 Webページでは数式を表すためにLaTeX表記が使えるMathJaxを利用します。
WebブラウザにはSafari/Chrome/Firefoxを使って下さい。
Webページでは数式を表すためにLaTeX表記が使えるMathJaxを利用します。
WebブラウザにはSafari/Chrome/Firefoxを使って下さい。
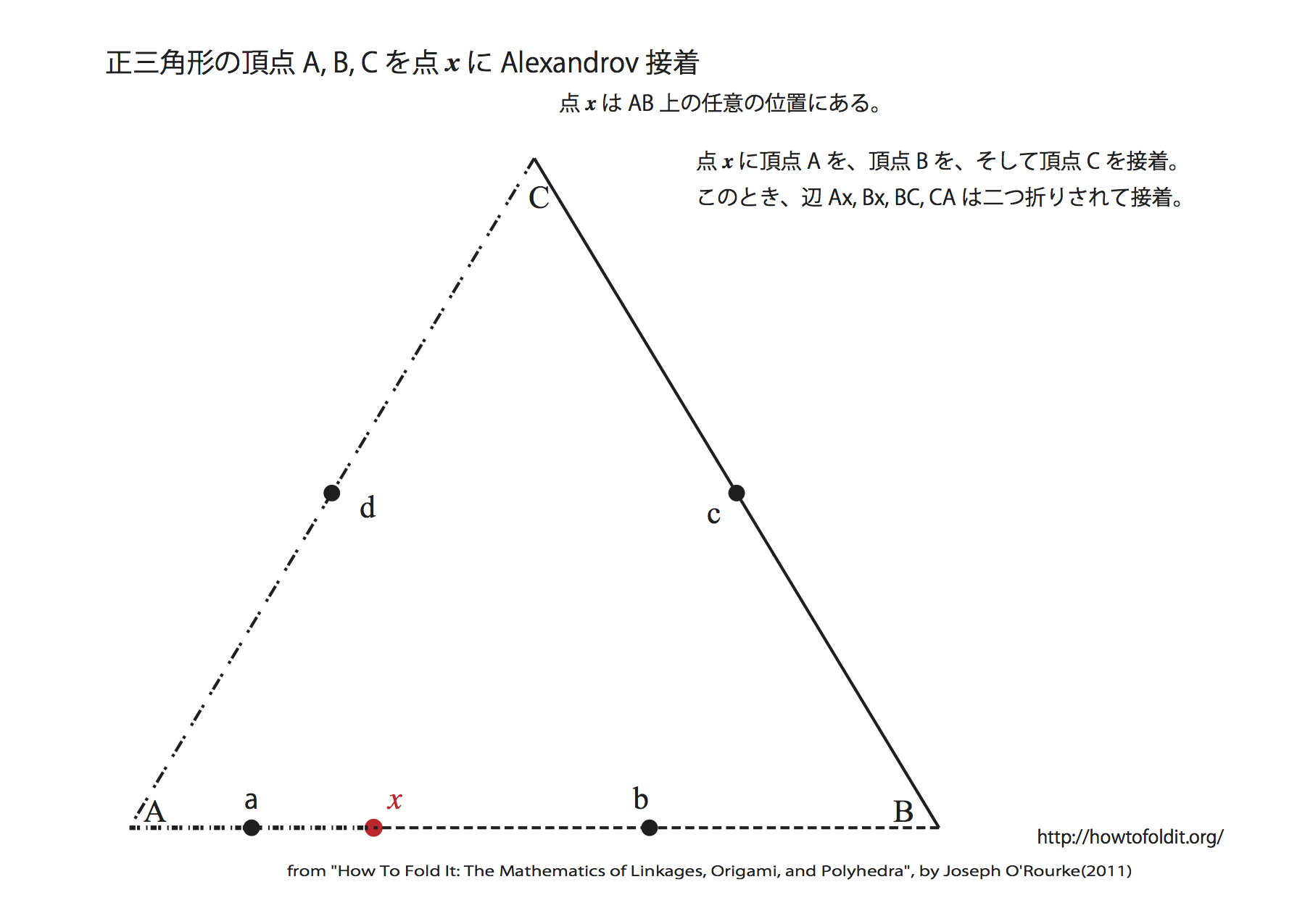
Alexandrovの展開定理
多角形のAlexandrov接着
次の3つの条件を満たす接着(glue)をAlexandrov接着という。
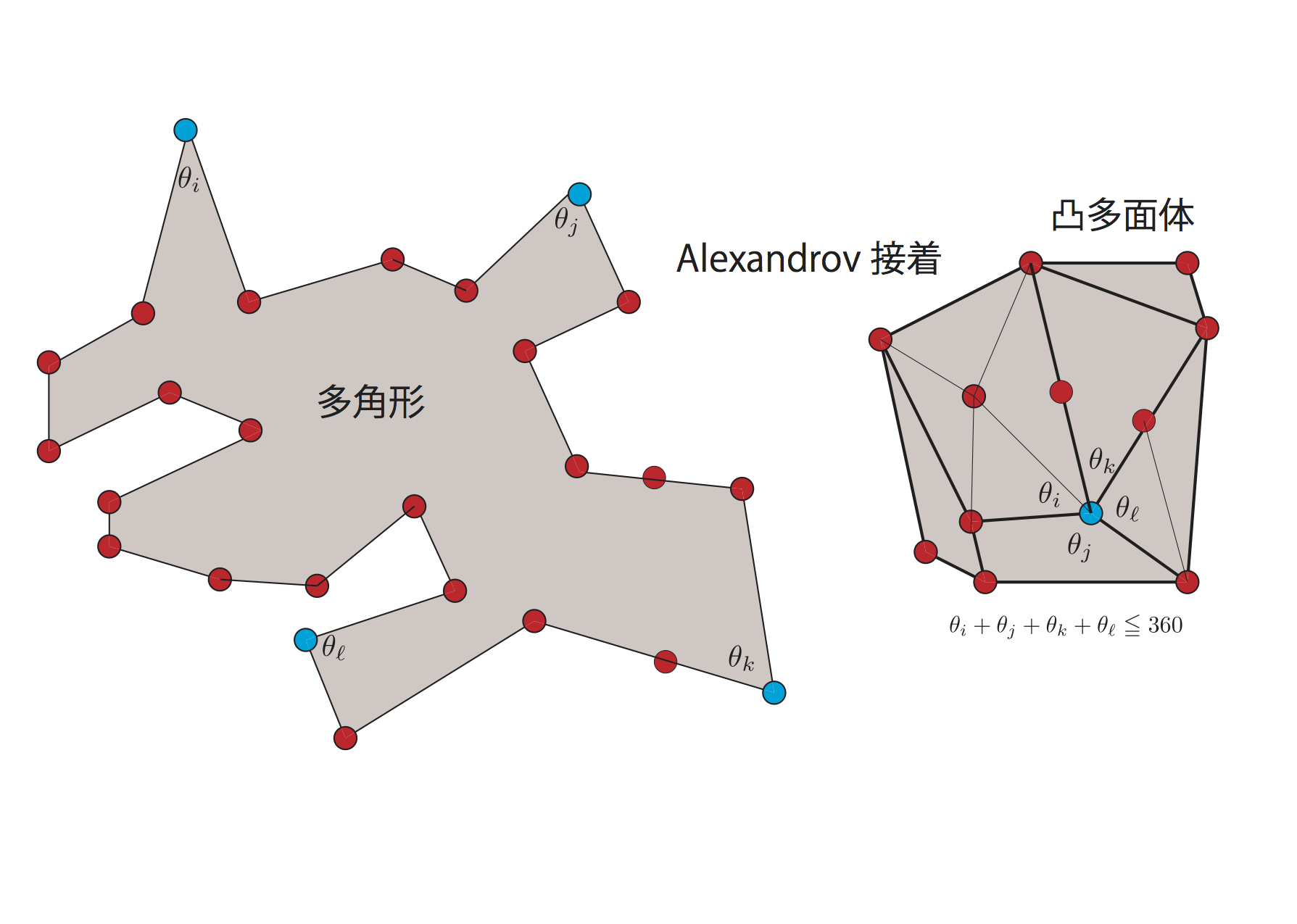
- 多角形の協会全てを使った接着。 自分自身を接着する(接着の不動点となる)孤立点も認める。
- 多面体を接着した継ぎ目部分は、接着した多面体の内部角度の合計が360°を越えない(得られる凸多面体が満たすべき条件)。 360°になるときには、接着面は角にならずに平面になって継ぎ目は消えてしまう)
- 接着で得られた多面体は球に同相(多面体の表見は球に連続変形でき、トーラスのような穴が空いていない)。
定理[Alexandrov(1948)]:
すべてのAlexandrov接着によって、得られる凸多面体は一意的に定まる。
(2重にカバーされた多角形も多面体と考えておく)。
多面体に折ってみる
from "How To Fold It: The Mathematics of Linkages, Origami, and Polyhedra", by Joseph O'Rourke(2011) http://howtofoldit.org/
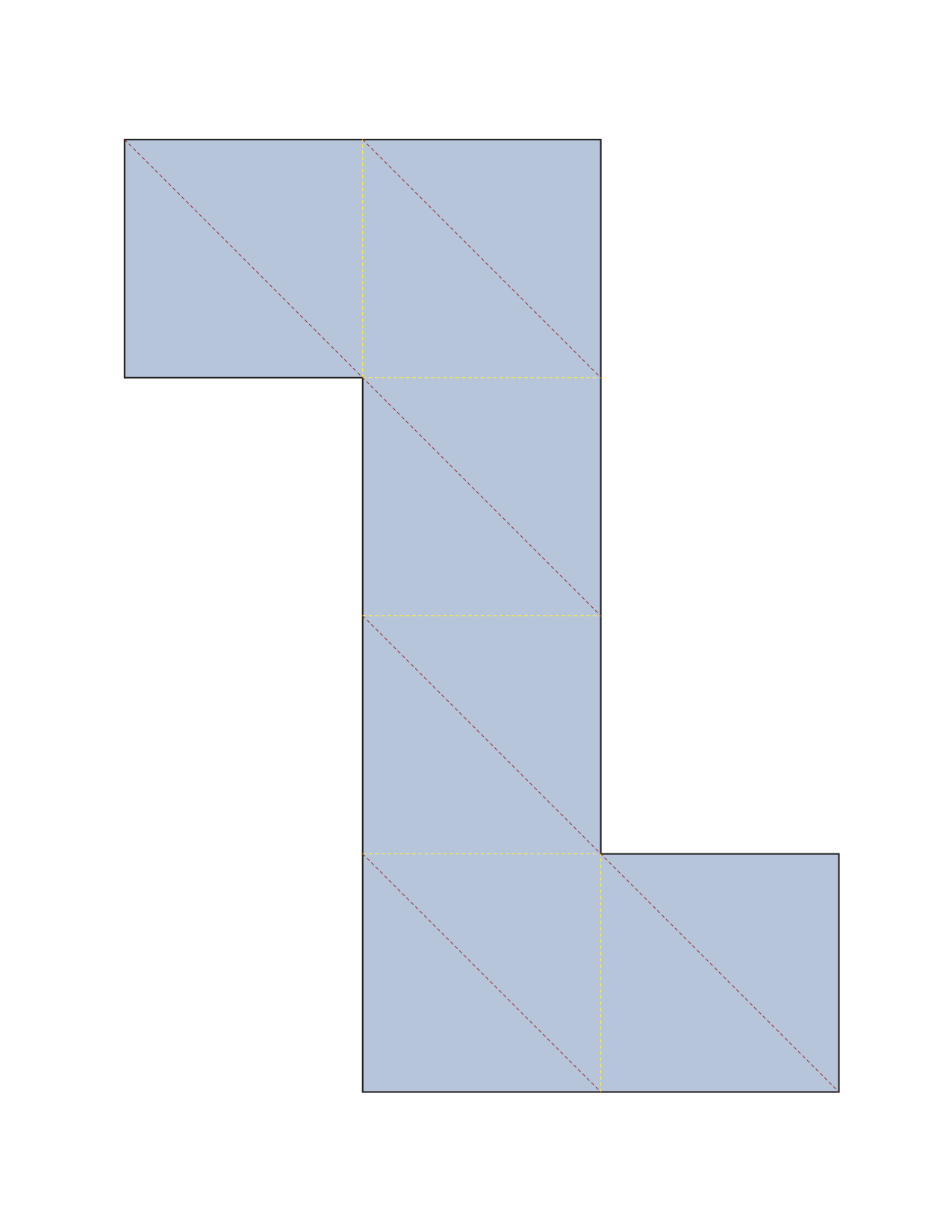
問題:
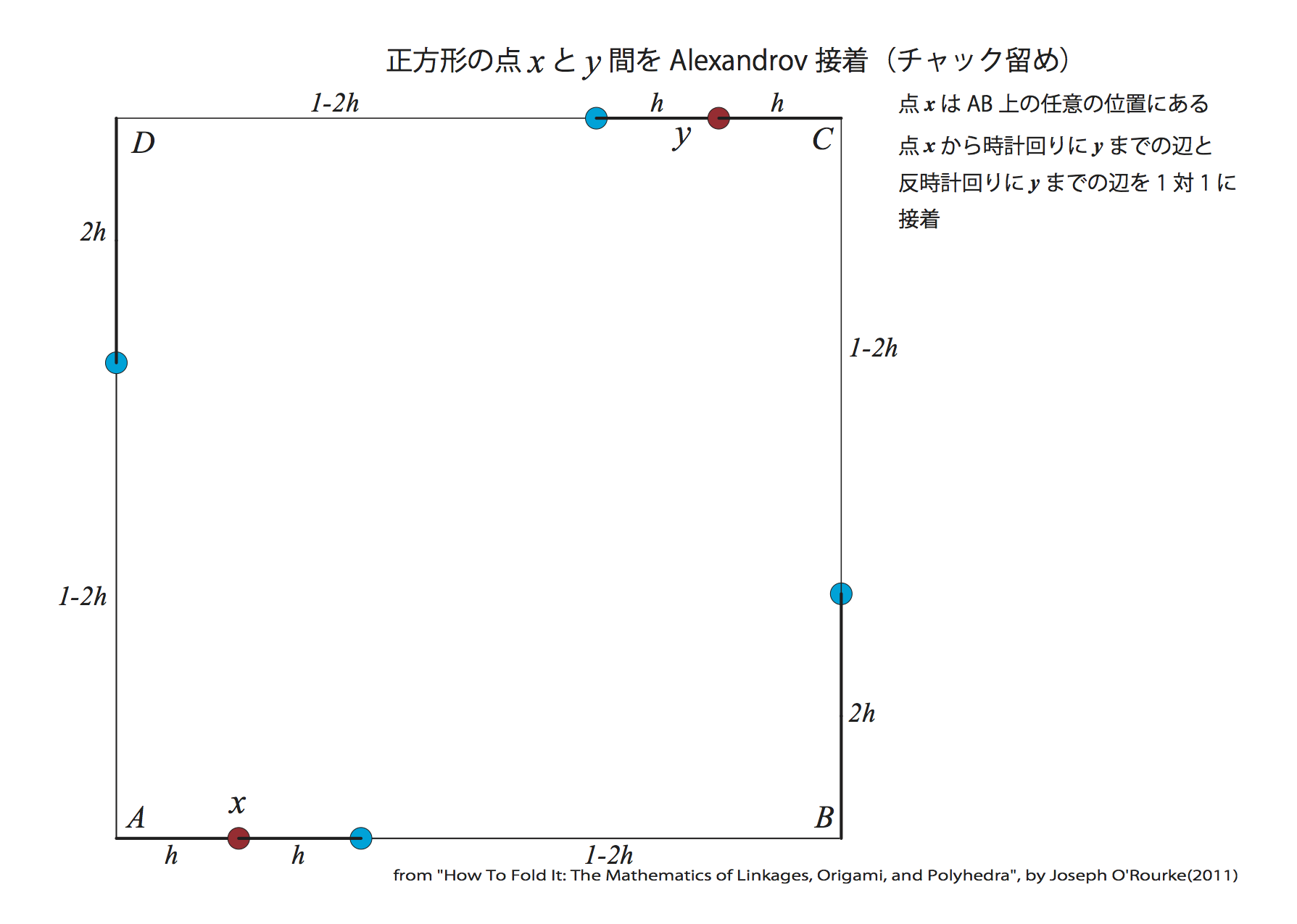 左図の展開図からAlexandrov接着させて、多面体を折る。
左図の展開図からAlexandrov接着させて、多面体を折る。
正方形の周囲に沿って$x$から反時計回りに位置する点と、$C$から反時計回りで同じ距離だけ移動した点$y$とを対応させて接着する(点$x$から時計回りに$y$までの辺と反時計回りに$y$までの辺を1対1に接着)。
 左図の展開図からAlexandrov接着させて、多面体を折る。
左図の展開図からAlexandrov接着させて、多面体を折る。正方形の周囲に沿って$x$から反時計回りに位置する点と、$C$から反時計回りで同じ距離だけ移動した点$y$とを対応させて接着する(点$x$から時計回りに$y$までの辺と反時計回りに$y$までの辺を1対1に接着)。
未解決問題
Platon多面体を切り開いて1つの多角形にしたとき、これを折って別のPlaton立体にすることができるか?
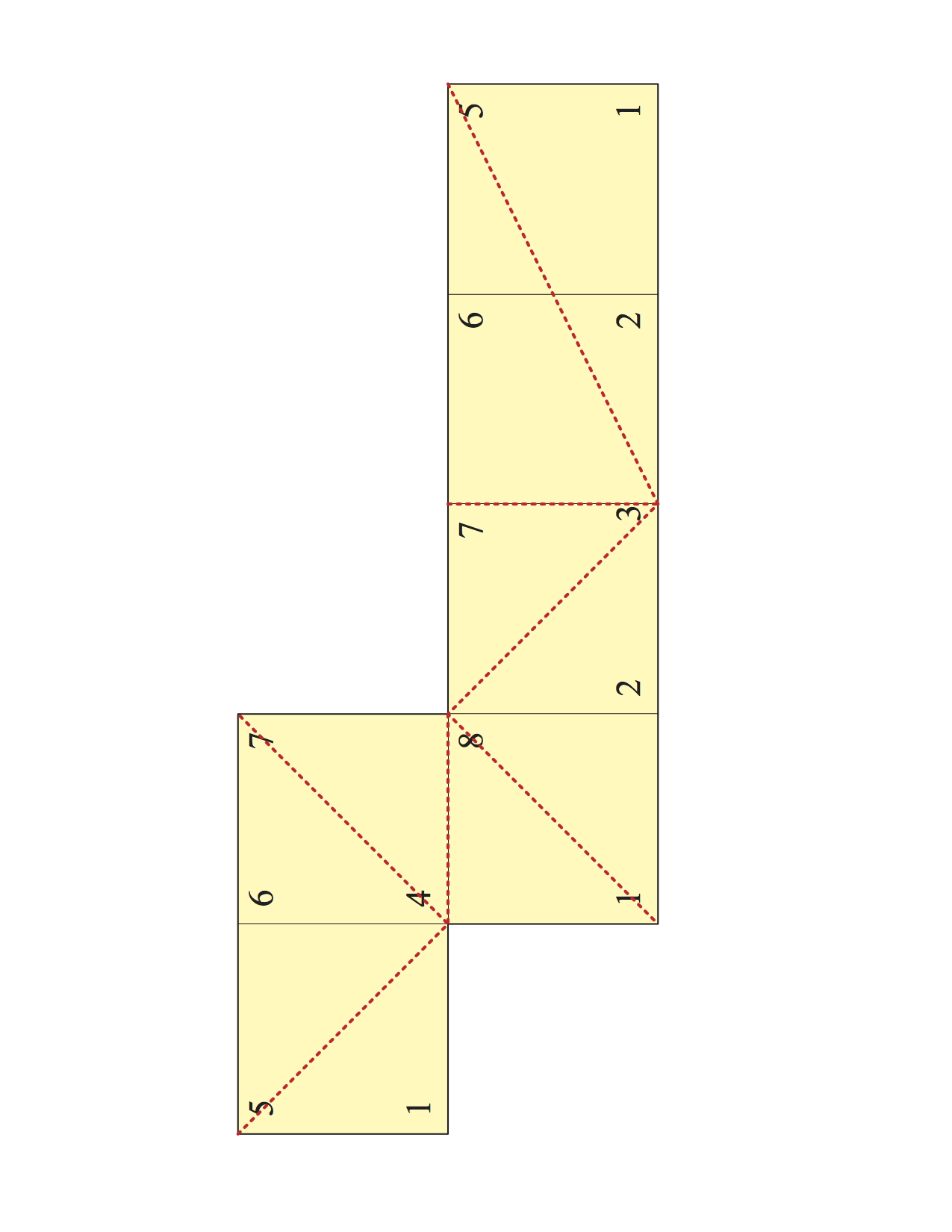
惜しい例1
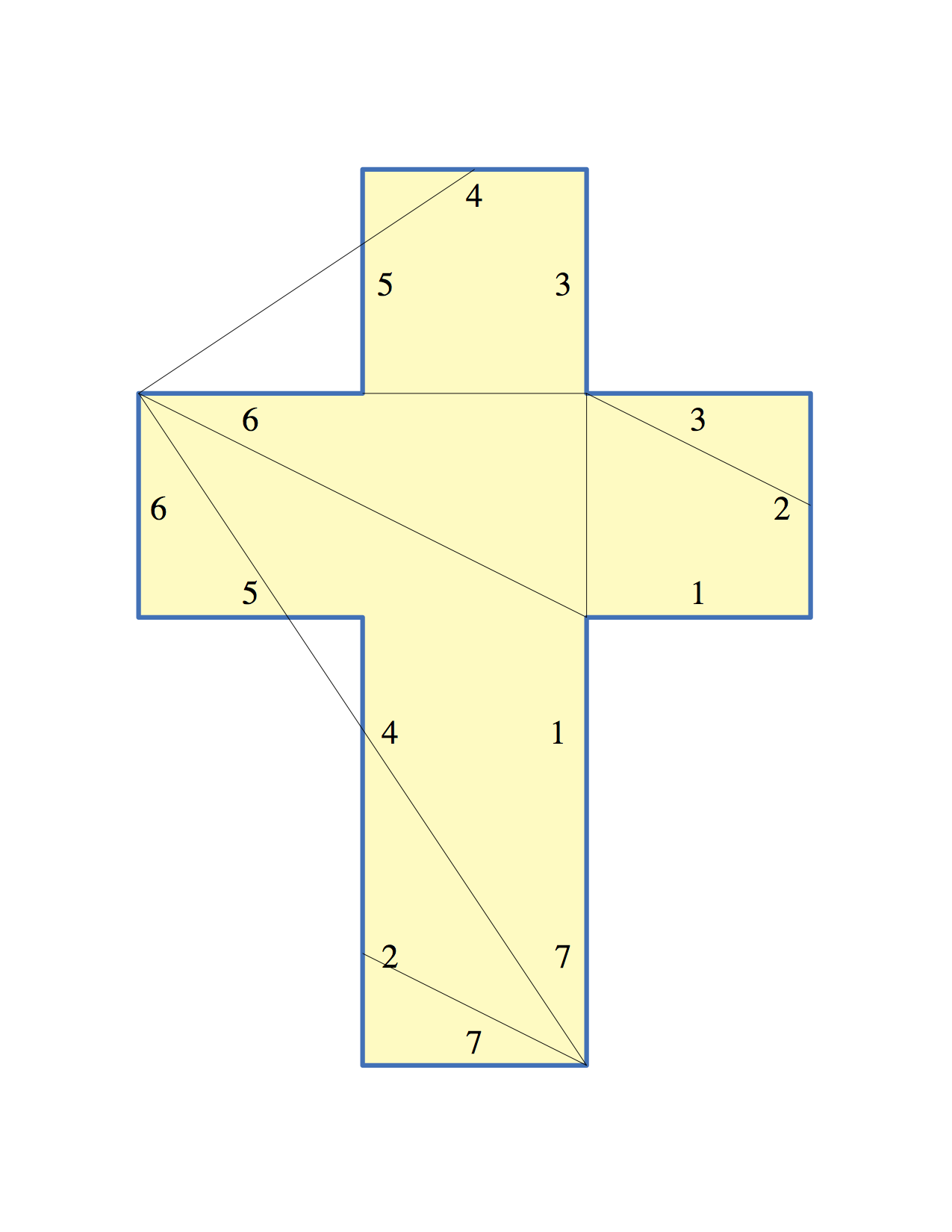
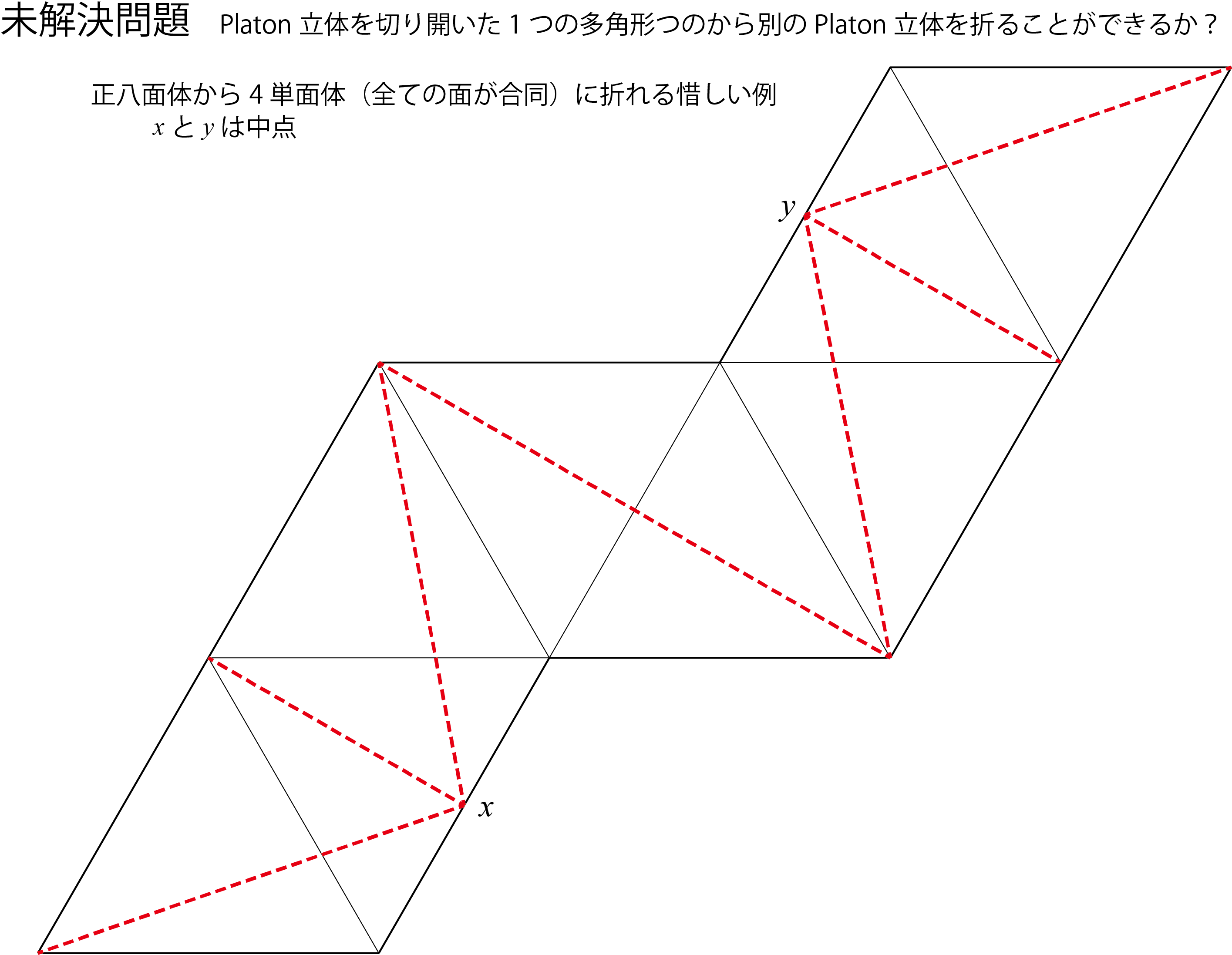 正四面体が4単面体(全ての面が合同)になる例。
点$x$と$y$は辺の中点。
正四面体が4単面体(全ての面が合同)になる例。
点$x$と$y$は辺の中点。
惜しい例2(平田の正4面体)
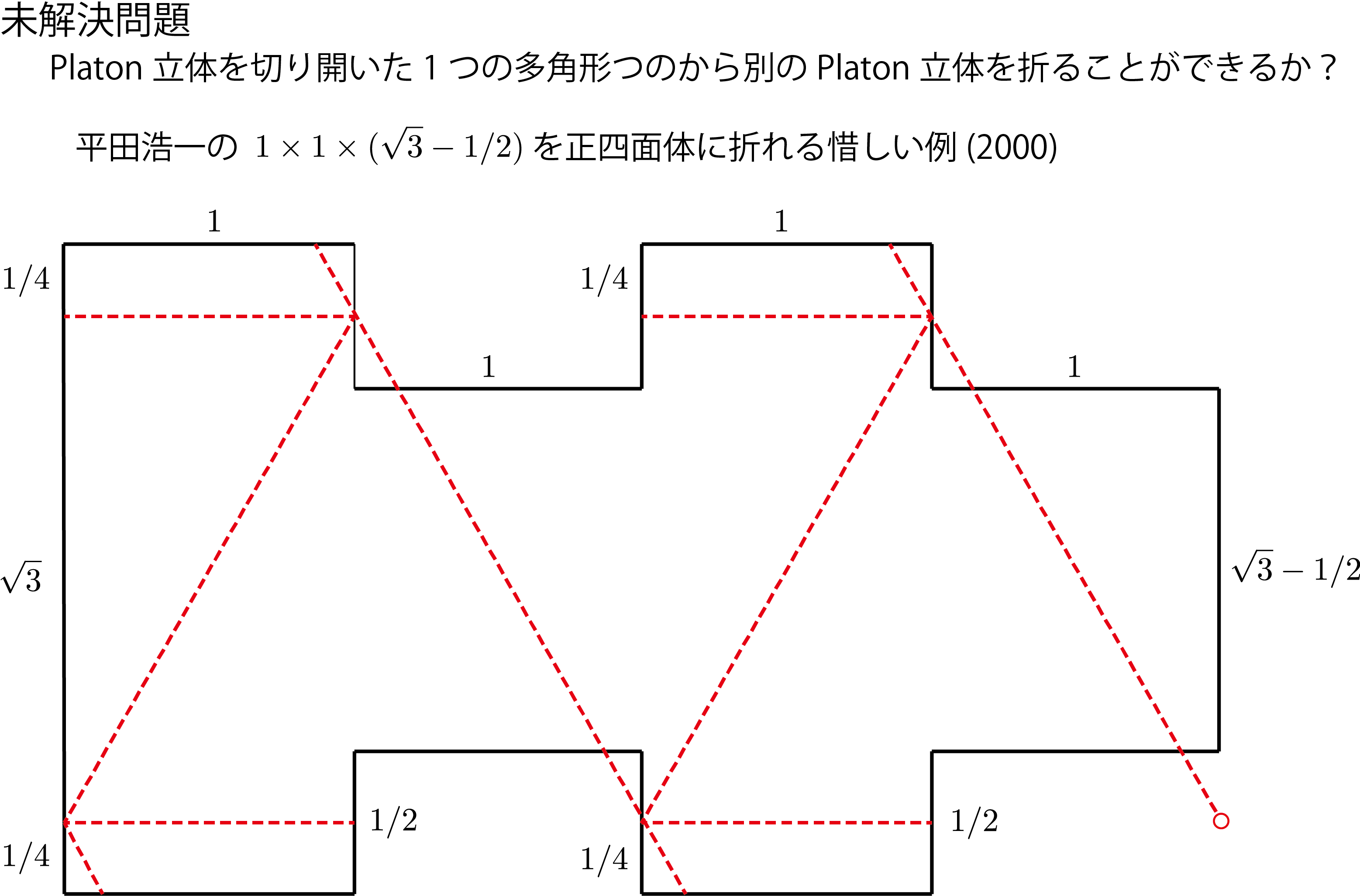 比$1:1:\sqrt{3}-1/2$の直方体が正四面体になる平田の例(2000年)。
比$1:1:\sqrt{3}-1/2$の直方体が正四面体になる平田の例(2000年)。