左メニューなどが狭く見づらくなった場合には､ウィンドウ幅を調節してみて下さい。
Webページでは数式を表すためにLaTeX表記が使えるMathJaxを利用します。
WebブラウザにはSafari/Chrome/Firefoxを使って下さい。
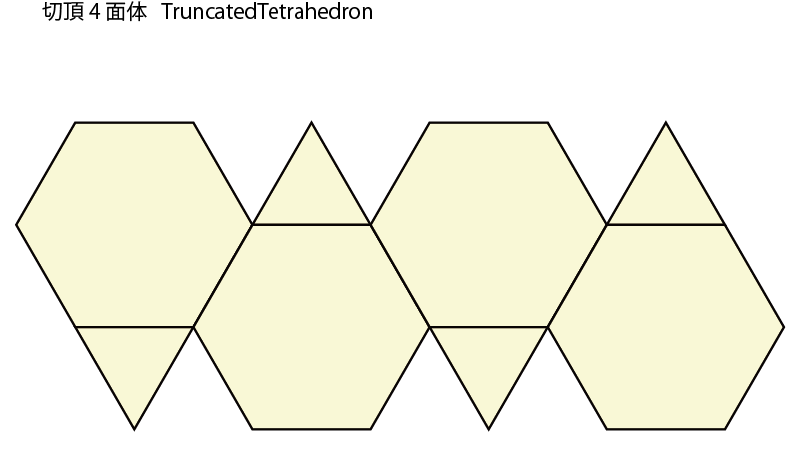
多面体の展開図
多面体の展開図(net)とは多面体の表面を平面上に重なることなく、しかも一つながりの多角形として描いたものである。 展開図から多角形を切り抜いて、適切に折り曲げて多角形を貼り合わせると元の多面体が復元できる。
多面体の辺に沿って切って、シワや破れなく平面上に展開した図を辺展開図(edge unfolding net)という。 一方、多面体の辺以外の任意の場所に切れ目を入れて平面上に展開した図を一般展開図(general unfolding net)と呼ぶ。 両者を区別しないときには、単に「展開図」という。
Dürerの「測定法教則」
1525年のAlbrecht Dürerの著作「測定法教則」(Underweysung der messung, mit den zirckel un richtscheyt, in Linien ebnen unnd gantzen corporen)には、 Viertes Buchにあるように、 多角形の作図法からはじめて、アルキメデス多面体などさまざまな多面体の展開図が載っている（書籍のPDFダウンロード）。
アルキメデス多面体
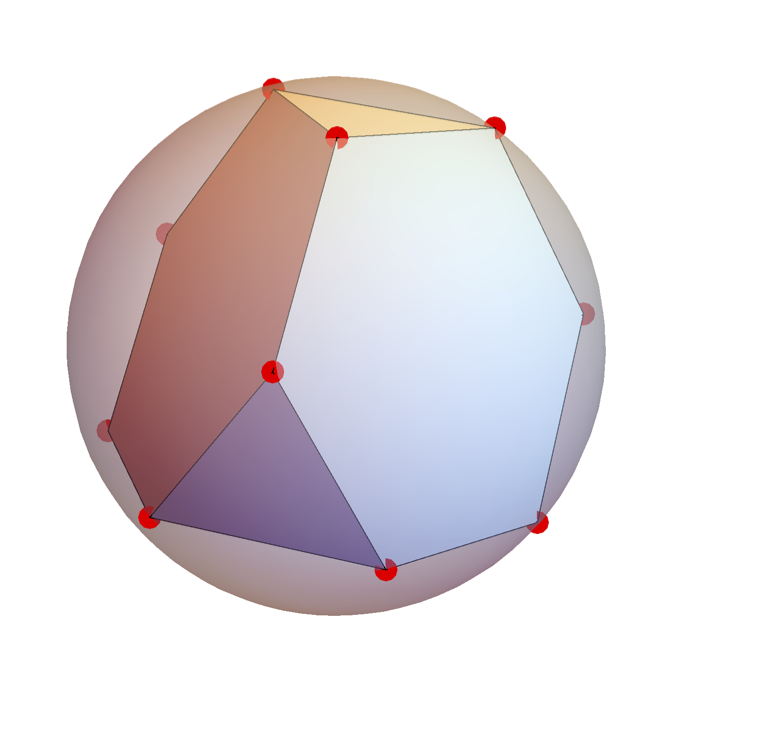
正多面体をプラトン多面体という。 全ての面が正多角形で、頂点に集まる正多角形の種類と順序が同じ（頂点形状が合同）であるような一様多面体でプラトン多面体以外の13種類の多面体を アルキメデス多面体(Archimedean solid)と呼ぶ。
左図はアルキメデス多面体の１つ切頂4面体(Truncated Tetrahedron)の辺展開図である。
切頂4面体の各頂点は球に内接していることを示しなさい。
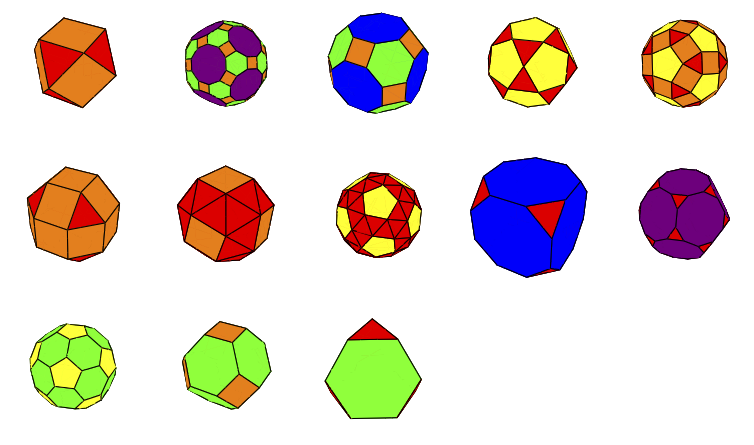
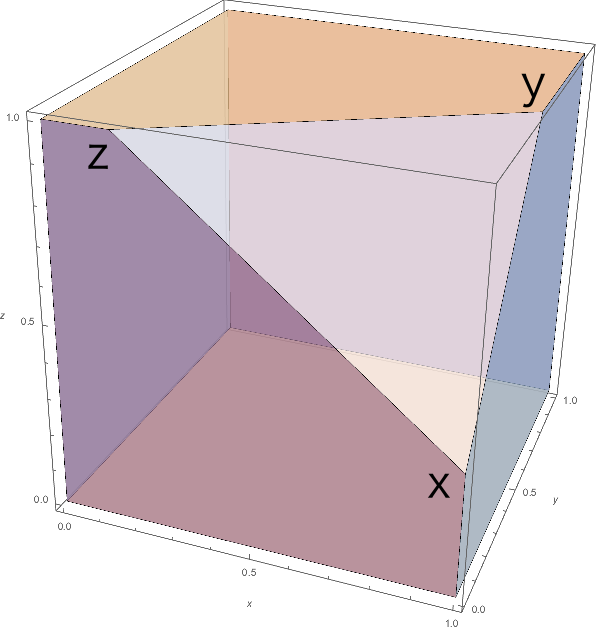
左図のように、辺の長さ1の正六面体の一部を、3点$x=(1, 0, 1/3)$, $y=(1, 1/2, 1)$, $z=(1/6, 0, 1)$を通る平面で切り取って得られた多面体を考える。
この多面体の辺展開を考え、一部が重なってしまう展開と重ならない辺展開の2つを描きなさい。
すべての凸多面体の辺展開図を常に描くことができるか？
ただし、プラトン多面体（正多面体）やアルキメデス多面体に対しては正しいことが解っている。
凹多面体（非凸多面体）については、展開図を持ち得ない例が知られているので、凸多面体に対して問題となる（Grunbaumの13面体の展開図を持ち得ない例）。
一般展開図
左図の展開図を多面体に折ってみよ。
左図の展開図を多面体に折ってみよ。
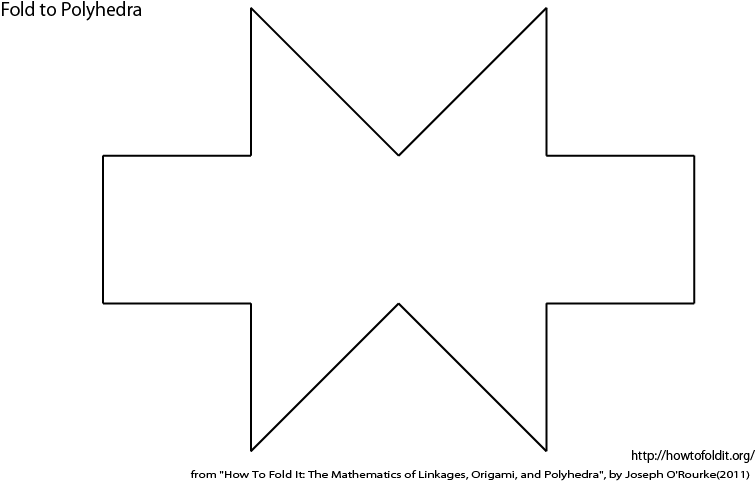
すべての凸多面体は辺展開図を持つかは未解決であるが、以下の星展開のように一般展開図なら持つことが知られている。
from "How To Fold It: The Mathematics of Linkages, Origami, and Polyhedra", by Joseph O'Rourke(2011) http://howtofoldit.org/
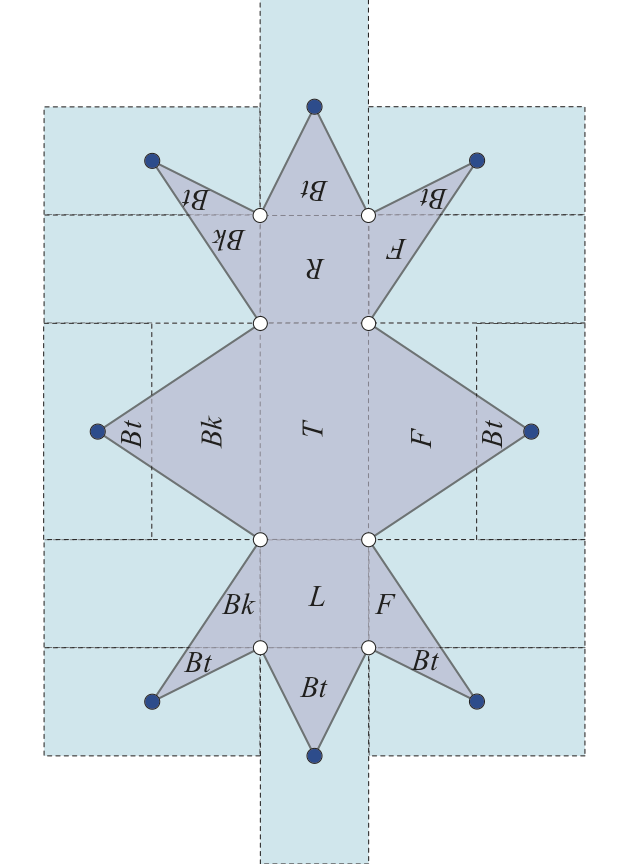
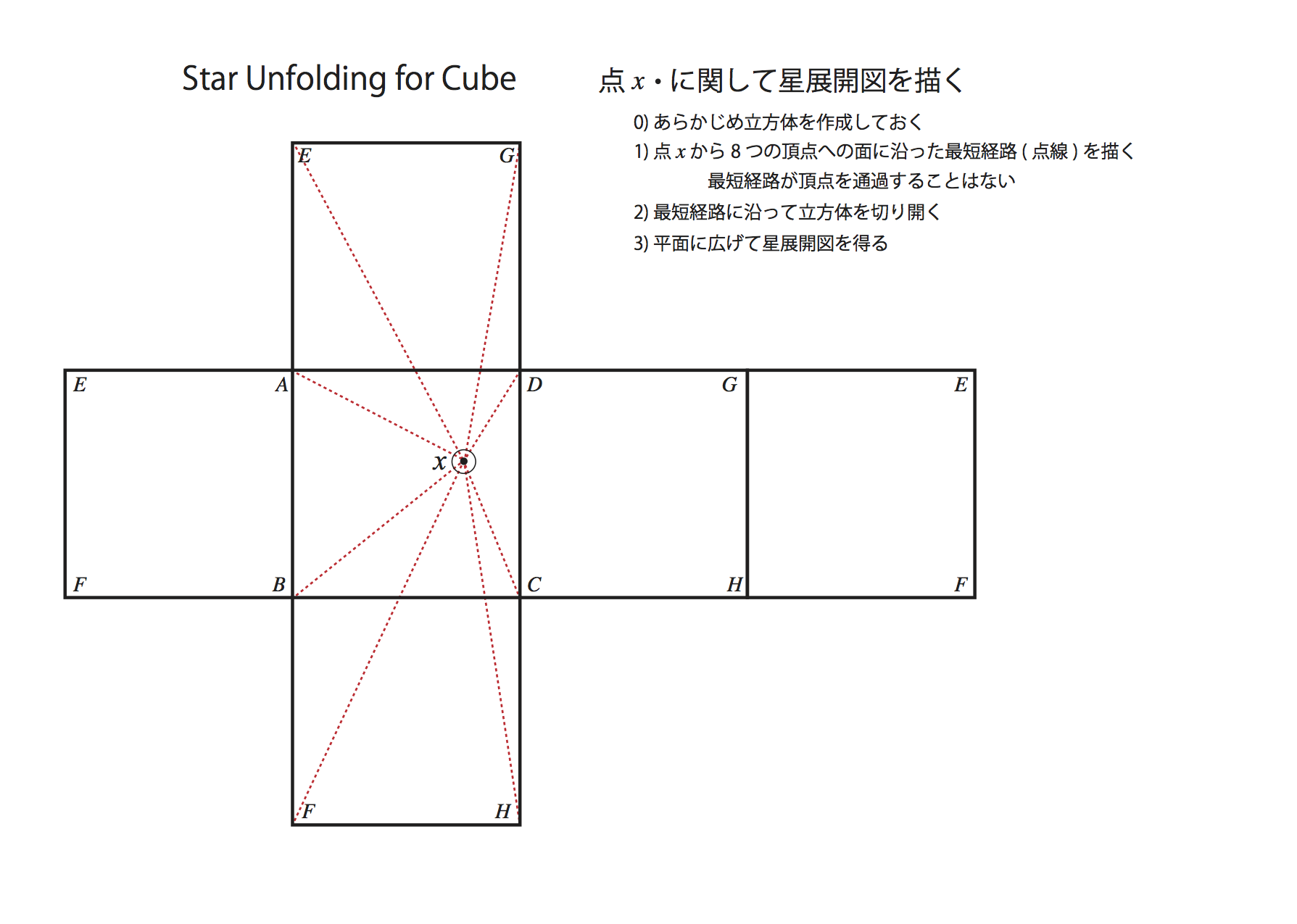
星展開(star unfolding)
凸多面体に対して、重なりを持たないような一般展開図をいつでも得る方法が2つ知られている。 1つは起点展開(source unfolding)もう一つが星展開(star unfolding)である。
星展開の方法とは、凸多面体上の点$x$から全ての頂点への最短経路(shortest path)に沿って多面体を切り開くやり方である。 ただし、多面体上の点$x$を各頂点への最短経路が一意的に定まるように選ばれている必要がある。
- 凸多面体上の頂点になる一般の点から、各頂点への最短経路は頂点から先に延びることはない （頂点を経由して，他の点に最短で到達することは凸多面体ではあり得ない）。
- 多面体上の最短経路が辺を横断するとき、展開図においては直線となっている。
右図の立方体の展開図を組み立てた上で、点xに関する星展開を実施して、星展開図を描いてみよ。
