スケールフリーネットワークの理解

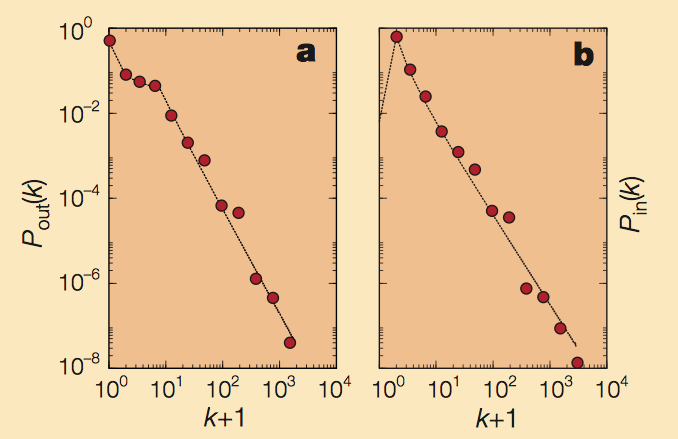
diameter_web caption_diameter_web

Albert-László BarabásiとRéka Albertは、Diameter of the world wide web（Nature 401, 130-131 (1999)）でWebページの外向きリンクと内向きリンクの双方に関するネットワーク構造の次数分布がベキ法則にしたがっていることを発見した（左図）。 右図は左図の説明で、頂点 $k$ を持つ次数分布 $P(k)\sim k^{-\gamma}$ として、$\gamma_{out}=2.45$, $\gamma_{in}=2.1$と評価している。


Barabási-Albertモデル

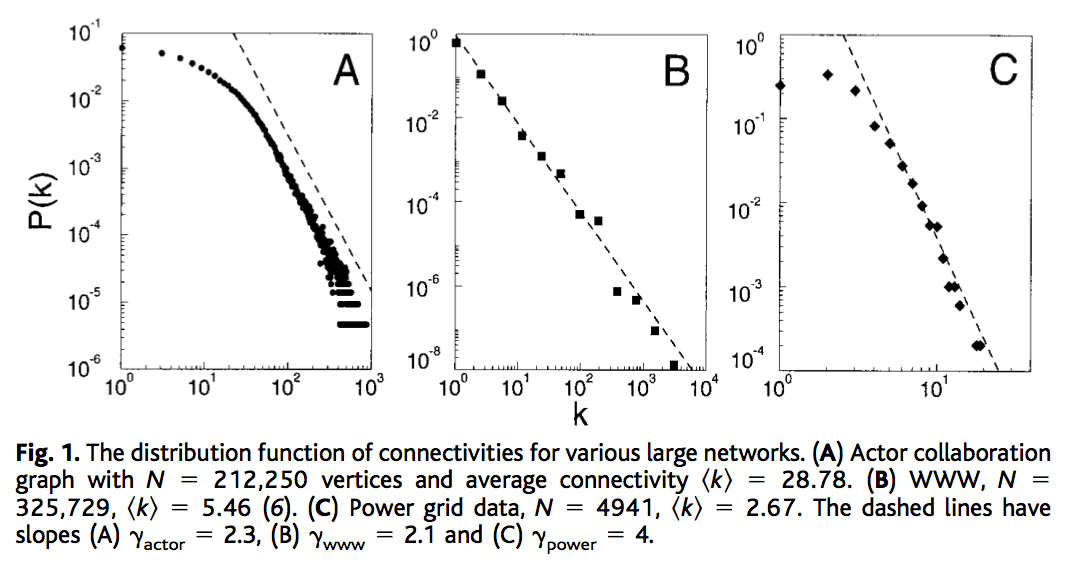
emergence_scalingfree

次いで、Albert-László BarabásiとRéka AlbertはEmergence of Scaling in Random Networks（Science 286, 509–512 (1999).）において、スケールフリーネットワークの形成モデルを提案した（今日では、Barabási-Albertモデルとも呼ばれている）。 Barabási-Albertモデルは、ネットワークのノード（頂点）が時間と共に増加していく成長ネットワークであることと、頂点次数の大きなノードが辺で接続されやすいという優先選択を特徴としている。

この論文では、左図のように、次数分布がベキ法則 $P(k)\sim k^{-\gamma}$ にしたがうようなネットワークとして、俳優の共演ネットワーク（$\gamma_{actor}=2.3$）、Webページ（$\gamma_{www}=2.1$）、電力グリッド（$\gamma_{power}=4$）を挙げている。


scalefree150-3

Mathematicaでは、Barabási-Albertモデルを使った BarabasiAlbertGraphDistribution[n,k] が、ステップごとに $k$ 本の辺を持つ新たな頂点が加えられて生成される $n$ 個の頂点を持つグラフ分布を得ることができる。 実際には関数 RandomGraph と併せて使う。 

RandomGraph[BarabasiAlbertGraphDistribution[150, 3]]

Barabási-Albertモデルに基づいて BarabasiAlbertGraphDistribution は、CycleGraph[3]（3角形を頂点にもつグラフ）から始まり、各ステップごとに $k$ 本の辺を持つ頂点が加えられるのであるが、その$k$ 本の辺は頂点次数に比例する分布にしたがってランダムに頂点に接続される。


次数分布をシミュレートする

BAモデルで生成されるグラフの次数分布を計算してみよう。 まず、ステップごとに $m=3$ 本の辺を持つ新たな頂点が加えられるとして、10万個の頂点をもつBAグラフを生成する。 

ba3 = RandomGraph[BarabasiAlbertGraphDistribution[10^5, 3]];

生成されたグラフ ba3 の次数分布は VertexDegree[ba3] で直ぐに与えられる。 ここで、ある未知の分布に従って、$n$個のデータ$x_1,\dots,x_n$ が生成されたとする（たとえば、この頂点の次数を考えればよい）。 この$n$個のデータが等確率（確率密度関数 $f(x)=\frac{1}{n}$）で起こるとする。 確率変数 $X$ が値 $x$ 以下となる分布関数 $F(x)$ が

\begin{gather*} F(x)=\frac{1}{n} \sum_{i=1}^n I(x_i < x),\\ I(x_i < x)= \begin{cases} 1, & x_i \leq x,\\ 0, & x < x_i \end{cases} \end{gather*}

で与えられるとき、この分布関数を経験分布関数といい、Mathematicaでは EmpiricalDistribution[...] で計算される。 つまり、グラフ ba3 の次数分布 empddistrBA3 は次で与えられる。 

empddistrBA3 = EmpiricalDistribution[VertexDegree[ba3]]
ba3

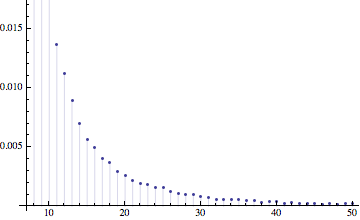
分布 dist の $x$ で評価された確率密度関数は Mathematicaでは PDF[dist, x] で与えられることを使って、次数分布 empddistrBA3 を次数 $k=7$ から $k=50$ までをプロットしてみた結果が左図である。 


DiscretePlot[PDF[empddistrBA3, k], {k, 7, 50}]

ここであがかれたデータ PDF[empddistrBA3, k] の先頭の10要素は次のようである。 

Take[Table[PDF[empddistrBA3, k], {k, 7, 50}], 10]
    {4737/100000, 1659/50000, 2419/100000, 1897/100000, 697/50000,
     253/25000, 223/25000, 363/50000, 18/3125, 499/100000}

LogLog表示からベキ分布を推測する

この次数分布 empddistrBA3 の描き方を変えて、横方向の次数 $k$ を $\log k$ で、縦方向の確率分布値 PDF[empddistrBA3, k] を $\log$PDF[empddistrBA3, k] で表したデータ loglogba3 としよう。 

loglogba3 = Table[{Log[PDF[empddistrBA3, k]], Log[k]}, {k, 7, 50}];

実際、loglogba3 の先頭の10要素は次のようになっている。 

Take[loglogba3, 10]
   {{-Log[100000/4737], Log[7]}, {-Log[50000/1659], Log[8]}, 
    {-Log[100000/2419], Log[9]}, {-Log[100000/1897], Log[10]}, 
    {-Log[50000/697], Log[11]}, {-Log[25000/253], Log[12]}, 
    {-Log[25000/223], Log[13]}, {-Log[50000/363], Log[14]}, 
    {-Log[3125/18], Log[15]}, {-Log[100000/499], Log[16]}}

この形のデータの組 $\{\{x_1,y_1\},\{x_2,y_2\},\dots,\{x_n,y_n\}\}$ に最もよくフィットする局前を最小二乗法によって求めてみよう。

まず、最も良くフィットする線を求めてみると、次のようになる。 

line = Fit[loglogba3, {1, x}, x]
    0.943341 - 0.34321 x

すなわち、データ loglogba3 は、直線にフィットさせると、直線 $y= 0.943341 - 0.34321 x$ に最適というのである。 次に、2次曲線にフィットさせてみると次の結果を得る。 

parabola = Fit[loglogba3, {1, x, x^2}, x]
    0.599171 - 0.462475 x - 0.00962642 x^2

すなわち、データ loglogba3 は、2次関数にフィットさせると、$y=0.599171 - 0.462475 x - 0.00962642 x^2$ に最適というのである。

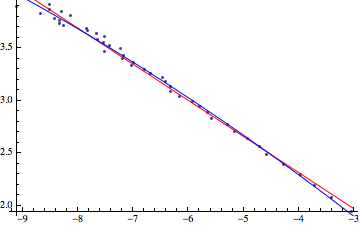
loglogfit

そこで、データ loglogba3 をプロットし、これに重ねて求めた直線を赤で、2次関数を青で描いてみた結果が左図である。

この結果からわかるように、次数分布 $P(k)$ を求めて Log-Log表示させると、一定値の傾き $-\gamma$ を持つ

\[ P(k)\sim k^{-\gamma} \]

に従う分布となっていることが分かる。 このような分布をベキ分布（power distribution）といい、定数 $\gamma >0$ をベキ指数（power index）という。


ヒストグラム表示

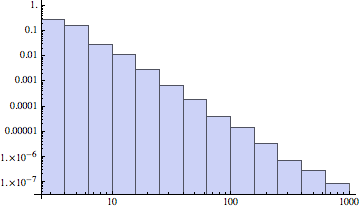
ba3_histgm

次数分布をヒストグラムとして、縦軸の確率（頻度）と横軸の頂点の次数をそれぞれ対数で取り直してLog-Logで表してのが右図である。 

Histogram[VertexDegree[ba3], {"Log", 10}, {"Log", "PDF"}]
このヒストグラムにおいても、指数 $\gamma$ を持つベキ分布と見なすことができる。

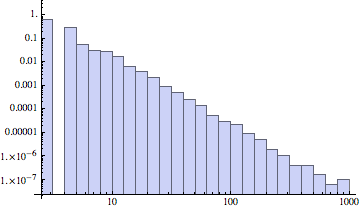
ba3_bin25

ヒストグラムの幅（ビン bin という）を変えて、 

Histogram[VertexDegree[ba3], {"Log", 25}, {"Log", "PDF"}]

としても、その傾きはほとんど変化しないことにも注意しておこう。


自律システムのネットワークの次数分布

Mathematicaでは、ネットワーク経由で自律システムのグラフデータを取得できる。 これをルータレベルのインターネット構造とみなそう。 

g = ExampleData[{"NetworkGraph", "Internet"}];

頂点数が 22963、頂点数に対する辺の数の割合（整数化）が2であることがつぎのようにわかる。 

VertexCount[g]
    22963
Round[EdgeCount[g]/VertexCount[g]]
    2

仮に、このグラフをBAモデルで記述できるとするならば、ステップごとに m=2 本の辺を持つ新たな頂点が加えられるとみなすのが合理的である。 

baInternet = 
   BarabasiAlbertGraphDistribution[VertexCount[g], Round[EdgeCount[g]/VertexCount[g]]]
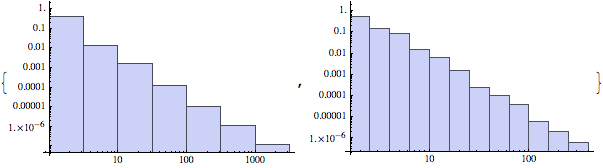
comapre_ba_internet

では、実際のグラフ g とBAモデルで生成したグラフ baInternet とを比較してみよう。 左が実データに基づいた次数分布、右がBAモデルに基づいて生成した次数分布であるが、両者の傾きはほぼ等しいことがわかる。 


{Histogram[VertexDegree[g], {"Log", 10}, {"Log", "PDF"}], 
 Histogram[VertexDegree[RandomGraph[baInternet]], {"Log", 10}, {"Log", "PDF"}]}

このことから、自律システムのインターネットのネットワーク構造は次数分布に関する限り、$m=2$としたBAモデルで説明できると考えられる。 ただし、頂点の総数 $n$の大域的クラスター係数（平均クラスター係数）$C$ は両者で次のように異なっている（）。 

N[GlobalClusteringCoefficient[g]]
    0.0111464
N[GlobalClusteringCoefficient[RandomGraph[baInternet]]]
    0.000847071

ここで、頂点の総数 $n$の平均クラスター係数 $C$ は頂点 $i$ のクラスター係数 $C_i$ を使って、次のように定義される量である。 ただし、$k_i$は頂点$i$の次数、$M_i$ は頂点 $i$ に隣接している頂点の集まり（頂点$i$から距離1にある頂点）間で接続されている辺の数とする。

\begin{gather*} C=\frac{1}{n}\sum_{i=1}^n C_i,\\ C_i= \frac{M_i}{{}_{k_i}\mathrm{C}_2} \end{gather*}

BAモデルの追加される辺の数 $m$ の依存性

自立システムのレベルにおけるインターネット構造をBAモデルとで比較する際に、ステップごとに追加される辺の数を $m=2$とした。 最初のBAモデルでは $m=3$ としてLog-Log次数分布を計算した。

このようにしてBAモデルで静止したグラフ構造の次数分布は一般的にどのようになるのだろうか。 また、Log-Log関係がベキ分布となるとしても、$m$ の選び方に影響されるのだろうか？

$m=2, 3$ 以外に $m=4$ でもシミュレーションしてみよう。 

ba2 = RandomGraph[BarabasiAlbertGraphDistribution[10^5, 2]];
empddistrBA2 = EmpiricalDistribution[VertexDegree[ba2]]

ba4 = RandomGraph[BarabasiAlbertGraphDistribution[10^5, 4]];
empddistrBA4 = EmpiricalDistribution[VertexDegree[ba4]]
ba2 ba4

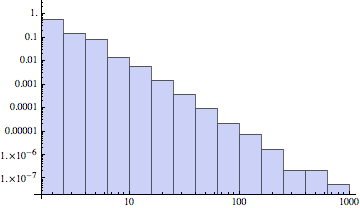
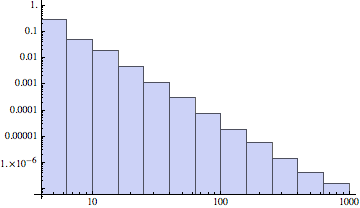
左側の図は$m=2$、右側の図は $m=4$ で生成したBAグラフのLog-Log次数分布である。 両者のLog-Log関係は同じ傾きを持つ直線と見なせることがわかる。