・大東のPC教室では、Matx・Octave・ScilabをWindowsマシン全てに導入済みです。
・自分のためのメモなので,下記に間違いがあっても,一切責任はとりません.空欄は単に調べていないだけ.
・OSは全てWindows NT4.0
| [1]パスの変更 | [2]行列の読み書き | [3]行列関数(基本) | [4]行列演算 | [5]記述統計関数 |
| [6]乱数・統計関数 | [7]ユーザー定義関数 | [8]簡単なグラフ | [9]非線型計画 | [10]Function Evaluation |
| Matx (ver. 5.2.16) | Octave (ver. 2.1.31) | Matlab (ver. 6.1) | Scilab (ver. 2.6) | |
| パスの変更 (z:\test へ) |
chdir("z:\\test") (注1) |
cd /cygdrive/z/test (注2) |
cd z:\test | chdir("z:\\test") (注3) |
| present working directory の表示 |
! cd (注4) |
pwd | ||
| ログファイルの作成と終了 | ? | ? | diary('ファイル名') diary off |
diary 'ファイル名' diary(0) |
(注1)\マークを読み取れる場合には,z:\testでも大丈夫だが,大東ではこれでないとだめ.
(注2)大東ではcygwinの中で実行するので,WindowsのZドライブは,cygdrive/zにマウントしてある.
(注3)single quotation 'z:\test' でも大丈夫(Scilabはどちらでも認識するようだ)
(注4)記号 ! はDosシェルに渡す記号.従って,!
dir とすれば,pwd内のファイル一覧が見える.
fopenなどのように3行使わないで,1行で済ますことのできる関数
| Matx | Octave | Matlab | Scilab | |
| テキストファイルから 行列を読み込んで,それをXとする. (注1) |
read X << "mat1.txt" (注2) |
load "mat2.txt" (注3) |
X=load('mat0.txt') |
X=fscanfMat('mat0.txt') |
| コマンドラインで, [1 2 3 5] を入力 |
X=[[1 2] [3 5]] | X=[1 2;3 5] | ||
| 行列Xの出力 | print X>>"ファイル名" (注2)' |
? | dlmwrite('ファイル名',X) | fprintfMat('ファイル名',X,'出力フォーマット') (注4) |
(注1)ファイル名をmat0.txtとして,プレゼントワーキングディレクトリにあるとしよう.
(注2)この場合,mat0からmat1を次のように書き換えねばならない.
(注2)'上記ファイルの形式で,行列が入れ替わり,行数と列数を表す数字が#とともに第1行に入る
(注3)この場合,mat0からmat2を次のように書き換えねばならない.
(注4)フォーマットは, %5.2f のような一般的な形.
| Matx | Octave | Matlab | Scilab | |
| 全部1の行列(m行n列) | ONE(m,n) | ones(m,n) | ||
| 全部0の行列(m行n列) | Z(m,n) | zeros(m,n) | ||
| 単位行列(m行m列) | I(m) | eye(m) | eye(m,m) | |
| Xのサイズ | size(X) | |||
| Xの行数 | Rows(X) | size(X,1) | ||
| Xの列数 | Cols(X) | size(X,2) | ||
行列同士の和や積は,X+Y,X*Yで共通
| Matx | Octave | Matlab | Scilab | |
| 行列Xと行列Yの, 成分同士の積と商 |
X.*Y X./Y |
|||
| 行列Xの逆行列(以下Xは行列) | inv(X) | |||
| Xの転置行列 | X' | |||
| Xとスカラーaの積 (Xの各成分にaを掛ける) |
a*X | |||
| Xのトレイス | trace(X) | |||
| 正方行列Xの行列式 | det(X) | |||
| Xとスカラーaの和 (Xの各成分にaを加える) |
a.+X | a+X | ||
| XとY(ともに行列)のクロネッカー積 | ? | ? | kron(X,Y) | ? |
| X対角成分を,列ベクトル化 | diag2vec(X) | diag(X) | ||
| 列ベクトルvの対角行列化 | vec2diag(v) | diag(v) | ||
| Xの固有値行列(A)と 固有ベクトルの行列(V) |
{A,V}=eig(X) | [V ,A]=eig(X) | [al,be,V]=gspec(X,eye(X)) (注1) |
|
(注1) al./be で固有値を表す列ベクトル.固有値行列にするには,A=diag(al./be);
Xは行列(m行n列とする)
yは列ベクトル(m行1列とする)
| Matx | Octave | Matlab | Scilab | |
| Xの全体の合計(答えはスカラー) | sum(X) | sum(sum(X)) | sum(sum(X)) | sum(X) |
| Xの列ごとの合計(答えは行ベクトル) | sum_col(X) | sum(X) | sum(X,'r') | |
| Xの行ごとの合計(答えは列ベクトル) | sum_row(X) | ? | sum(X,2) | sum(X,'c') |
| Xの列ごとの平均 | mean_col(X) | mean(X) | mean(X,'r') | |
| Xの列ごとの不偏分散(もしくは標準偏差) | std_col(X) (注1) |
std(X) (注1) |
var(X) | ? |
| yの不偏分散 | std(y) (注1) |
? | var(y) | ? |
(注1) 標準偏差を返す.
Excelも含める
| Matx | Octave | Matlab | Scilab | Excel2000(ワークシート上) | |
| U[0,1)に従う一様乱数の 行列(m行n列) |
rand(m,n) | rand(m,n) もしくは rand(m,n,'uniform') |
=rand() | ||
| 標準正規乱数 | randn(m,n) | rand(m,n,'norm') | =norminv(rand(),0,1) | ||
| 正規分布の密度関数 X〜N(m,s^2)として X=kの時の密度関数の値 φ[(k-m)/s] |
なし | normal_pdf(k,m,s^2) (注1) |
normpdf(k,m,s) (注3) |
なし | =normdist(k,m,s,false) |
| 正規分布の分布関数 X〜N(m,s^2)として X=kの時の密度関数の値 Φ[(k-m)/s] |
なし | normal_cdf(k,m,s^2) (注1) |
normpdf(k,m,s) (注3) |
cdfnor("PQ",k,m,s) | =normdist(k,m,s,true) |
| N(m,s^2)正規分布の逆関数 X〜N(m,s^2)として,Pについて, (X-m)/s=Φ-1(P) となるようなXの値を求める. |
なし | normal_inv(P,m,s^2) (注2) |
norminv(P,m,s) (注3) |
cdfnor("X",m,s,P,1-P) | =norminv(P,m,s) |
(注1) Xは行列でなければならない.normal_pdf(Xの値,平均,分散) というように第3引数は標準偏差でなく分散
(注2) Pは行列.スカラーの場合は,標準正規分布の逆関数のみ可能で,normal_inv(P)と引数はPのみ.
(注3) Statistical Toolboxが必要
| Matx | Octave | Matlab | Scilab | |
| 推奨拡張子 | .mm | .m. | .sci | |
| 関数の書き方 (最小2乗推定量の場合) 関数 myols 行列Xmat(m行n列)とyvec(m行1列)を インプットして,そのOLS推定量を返す関数 |
Func Matrix myols(Xmat,yvec) Matrix Xmat,yvec; { Matrix b; b=inv(Xmat'*Xmat)*Xmat'*yvec; return b; } |
function b=myols(Xmat,yvec) b=inv(Xmat'*Xmat)*Xmat'*yvec; |
||
| 関数を使うためには 保存名(myols.mm, myols.m, myols.sci) として上のプログラムが,PWD上で保存してあるとする. |
コマンドプロンプト上で, load "myols.mm" 書けば,その後使うことができる. |
PWD上にmyols.mが保存されて いるので,そのまま使える. |
コマンド上で, getf("myols.sci") と書けば,その後使うことができる. |
|
| 実行の様子. (X=[1 1 1]' y=[4 5 6]' としたので,答えはyの平均値となる.) |
 |
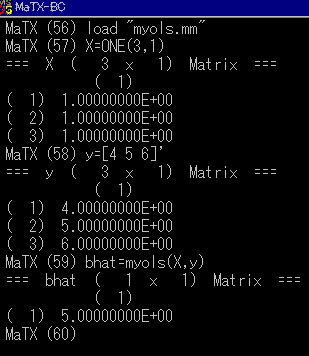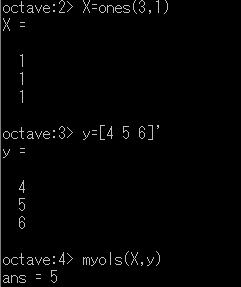
 上記はOctaveの様子 |
-->getf("myols.sci") -->X=ones(3,1) X = ! 1. ! ! 1. ! ! 1. ! -->y=[4 5 6]' y = ! 4. ! ! 5. ! ! 6. ! -->bhat=myols(X,y) bhat = 5. |
|
| Matx | Octave | Matlab | Scilab | |
| グラフのプロット(1) ２つの行ベクトルx,y (xとyの長さは同じ) |
gplot(x,y) | plot(x,y) | plot(x,y) | |
| グラフのプロット(2) 行ベクトルx,行列y (xとYの列数は同じ) |
なし | |||
| グラフのプロット(3) ２つの列ベクトルx,y (xとyの長さは同じ) |
なし | ? | plot(x,y) | plot(x,y) |
| グラフのプロット(4) 列ベクトルx,行列y (xとYの行数は同じ) |
なし | ? | plot(x,y) | plot2d(x,y) |
| Matx | Octave | Matlab | Scilab | |
| ベクトル方程式 ftest(x)=0を解く. (初期値 x0) |
なし | [x,info]=fsolve("ftest",x0) 注1) |
[x,v,info]=fsolve(x0,ftest) 注2) |
|
| 最小値を求める Y=argminx[ftest(X)] (初期値 x0) |
なし | Y=fminsearch('ftest',x0) |
注1) info=1の場合正常終了
注2) info=1の場合正常終了.vは終了時の値(かなり0に近い)
| Matx | Octave | Matlab | Scilab | |
| 関数ftest のxの値を,ftest(x)以外で求める | feval("ftest",x) | feval(x,ftest) (注1) |
||
(注1)xはスカラーのみ有効.ベクトルのときは,期待する値にならない場合がある.
修正 2003年05月20日, (c) Tamotsu KADODA