地球を測ろう

小説『世界の測量ガウスとフンボルトの物語』で登場する数学史上最大の数学者の一人 Johann Carl Friedrich Gauß(1777-1855)は曲面の幾何学にも取り組み多くの偉大な結果を得ている（たとえば、ガウス曲率に関するGauss-Bonnetの定理など）。

Gaussは地球の測量についても大いなる業績を上げた。球面上の三角測量（三角形群が平面にあるとして考えた三角測量では不正確な結果をもたらす）はオランダのSnell(光の屈折のスネルの法則の発見者。1580-1626)によって精密化されて以来、1745年にはフランス全土の地図が作成されている（既に、地球の大きさはほぼ分かっていた）。以降、ナポレオン帝政時代のJean Joseph Tranchot（1801）やGaussなどによって地球上の大規模な三角測量は精密化されていった（Gaussは、その過程で最小二乗法をも考案した）

地球の1/4周を一万Kmとしたのがメートル[m]の始まりである。 1791年フランスの科学アカデミーは、地球の赤道と北極点の間の海抜ゼロにおける子午線弧長を1/10000000倍した長さを1mと定義したのである（こうしてパリに16基のメートル原器が置かれた。現在のメートル原器は1879年に白金90%、イリジウム10%の合金で作られ、パリの国際度量衡局に保管されている）。

2点間の緯度経度から距離を計算する

地球が球体であると考えよう。以下の計算を理解するためには、初等的であるが多少の知識が必要である。以降の計算における角度は、10進角度と次の関係にあるラジアン角で測ることにする。 \[ \mbox{ラジアン角}=\frac{\pi\times \mbox{10進角度}}{180} \]

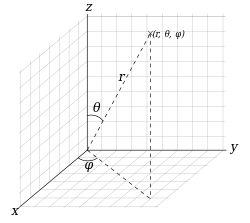右図の3次元極座標表示（球面座標系） $(r,\varphi, \theta)$ においては、地球の中心から北極軸を基準に z軸を、赤道面にx-y平面をとり、北極に向いた角度を$\theta=0$とする。 $0\leqq \pi/2-\theta\leqq\pi/2$の範囲の角度 $\Theta\equiv \pi/2-\theta$ を北緯（ north latitude：赤道面を北緯0度として北極方向が北緯90度）、$\pi/2 \leqq \theta \leqq \pi$ のとき、$\Theta\equiv \theta - \pi/2$ を南緯（south latitude）という。また、ロンドンの旧グリニッジ天文台を通過する北極と南極を結ぶ大円から東に向かう$0\leqq \varphi\leqq \pi$にある角度を東経（east longitude）、西に向かう角度を西経（west longitude）という。

このとき、北緯と東経で与えられた地球面上の位置$P$は、地球を半径 $R_e=6378.137$[km] の真球とすると、球面座標系とは $P=(R_e, \varphi, \pi/2-\Theta)$ の関係にある（球面座標系では北極軸を0度にして赤道面に向かって角度$\theta$を測ることを思い起こそう）。赤道面を0度として測る緯度 $\Theta$ と混同しないように。

したがって、位置 $P$ の球面座標系 $(R_e, \varphi, \theta)$ と直交座標系 $(x, y, z)$ との関係は次式で表される。 \begin{align} x &= R_e\sin(\pi/2-\Theta)\cos\varphi=R_E\cos\Theta\cos\varphi,\\ y &= R_e\sin(\pi/2-\Theta)\sin\varphi=R_E\cos\Theta\sin\varphi,\\ z &= R_e\cos(\pi/2-\Theta)=R_E\sin\Theta \end{align} である。南緯は$\pi/2\leqq \theta\leqq \pi$、西経は$-\pi\leqq \varphi\leqq 0$の場合と考えることにしよう。ちなみに、同じ経度の地球上のライン（大円）を子午線（meridian)という。地球を真球と見なしたとき、その子午線弧長は約40008kmである。このとき、度糞秒で測る距離単位は次のようになっている。
- 緯度1度の長さ約111km
- 緯度1分の長さ約1.85km
- 緯度1秒の長さ約30.9m
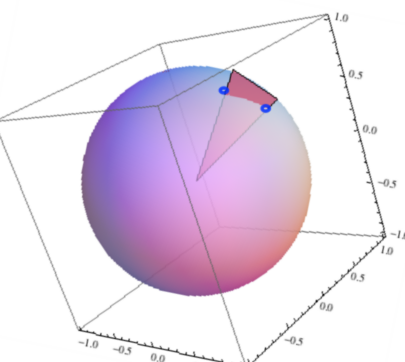
さて、地球の2点$P_1$と$P_2$間の緯度と経度がわかったとすれば、その2点を通過する大円（球の中心を通る平面が球面と交差するときに生ずる球面の切り口）が確定する。つまり、右図のように球面表面上にある2点に対する大円に沿った中心からの角度$\Theta_{12}$[ラジアン]が定まる。地球の半径$R_e=6378.137[{\rm km}]$を使うと、地球表面に沿った2点$P_1$と$P_2$間の距離は $R_{12}=R_e \Theta_{12}$となる。

$\Theta_{12}$を求めよう。 2点が球面にあるときには次の簡便な方法が使える。つまり、ベクトル$\vec{a}=(a_x, a_y, a_z)$と$\vec{b}=(b_x, b_y, b_z)$の内積$\langle \vec{a},\vec{b} \rangle$ \[ \langle \vec{a},\vec{b} \rangle = a_xb_x + a_yb_y +a_zb_z \] と、ベクトルのなす角度$\theta_{ab}$とは \[ \langle \vec{a},\vec{b}\rangle=|\vec{a}|\cdot|\vec{b}|\cos\theta_{ab} \] の関係にある。ここで、たとえば、ベクトル $\vec{a}$ の長さは $|\vec{a}| =\sqrt{a_x^2 + a_y^2 +a_z^2}$ としている。したがって、2つのベクトルがなす角度$\theta_{ab}$は、$\cos$の逆関数 $\cos^{-1}$ を使って \[ \theta_{ab}=\cos^{-1}\frac{\langle \vec{a},\vec{b}\rangle}{|\vec{a}|\cdot|\vec{b}|} \] と計算できる。

つまり、地球の2点 $P_1$と$P_2$間の球面上の距離を求める手続きは次のようになる。まず、地球面上の2点の緯度経度から上の球面座標系との関係式をつかい、直交座標表示 $\vec{P_1}=(x_1,y_1,z_1)$, $\vec{P_2}=(x_2,y_2,z_2)$の2ベクトルを計算する。次に、この2ベクトルの内積 \[ \langle \vec{P_1},\vec{P_2}\rangle \equiv x_1\cdot x_2+ y_1\cdot y_2 + z_1\cdot z_2 \quad (=\cos \Theta_{12}) \] を計算して、2地点のベクトルをなす角度を $\Theta_{12}=\cos^{-1} \displaystyle\frac{\langle \vec{P_1},\vec{P_2}\rangle}{|\vec{P_1}|\cdot|\vec{P_2|}}$ [ラジアン]として求める。このとき、求める地球の2点$P_1$と$P_2$間の地球表面に沿った距離 $R_{12}$ は \[ R_{12}=R_e\cos^{-1} \frac{\langle \vec{P_1},\vec{P_2}\rangle}{|\vec{P_1}|\cdot|\vec{P_2}|} \] で与えられる。もちろん地球は完全な球体ではなく、近似的には自転によって赤道方向に扁平な回転楕円体であると考えられる（精密な測定によって本当の地球の姿は西洋梨のような歪な姿をしていることがわかっている）。緯度経度を用いた2点間の計算は、少なくとも地球が球ではなく回転楕円体であることを考慮してさらに精密化する必要がある。

Google Mapsで指定地点の緯度・経度を調べる

以下の手順でGoogle Mapを使うとマウスでポイントした地点の緯度経度（および住所）を調べることができる。

Google Maps上で、緯度・経度を調べたい地点で右クリック
メニューから「この場所について」を選択
検索バーに緯度・経度が表示、サイドバーのところには郵便番号・住所が表示

さらに、効率よく利用するにはGoogle GeoCoding APIで提供されているGoogleのアドレスマッチングサービス『住所から緯度経度を一括変換するツール – NAPZAK』のようなWebサービスを使ってもよい。

計算例

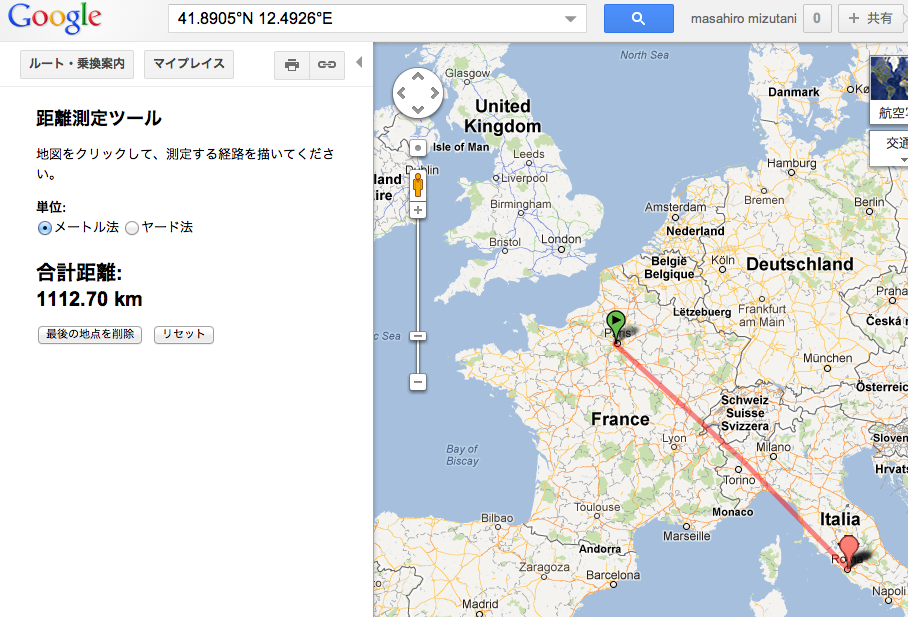Result of distance ローマのコロッセオの場所（10進度数角：北緯 48.829322 度, 東経 2.220172 度 / 度分秒角：北緯 48°49'45.552"、東経 2°13'12.619"）とパリの度量研究所の場所（10進法：北緯 41.8905 度, 東経 12.4926 度 / 度分秒角：北緯 41°53'25.8"、東経 12°29'33.36"）との2点間の直線距離は（ここでは安直に）距離サービスによって次を得ることができる。

「Google Map」では、1112.70km
「２地点間の距離と方位角」では、1,112.723562Km、
「距離と方位角の計算」（楕円体GRS80）では、1,112,833.273(m)

これらの結果と、上の[2点間の緯度経度から距離を計算する]方法で計算した結果とを比較してみよう。

以下に、上記の計算をRで実行した結果を掲げておく。最後の結果 1112.724 [Km] が計算によって求めた2点間の距離である。

> h1 = 48.829322 * pi / 180   <- コロッセオの緯度 h1: 10進度数緯度をRadian角に変換
> t1 = 2.220172 * pi / 180    <--           経度 t1: 10進度数経度をRadian角に変換
> h2 = 41.8905 * pi / 180     <- 度量研究所の緯度 h2: 10進度数緯度をRadian角に変換
> t2 = 12.4926 * pi / 180     <--           経度 t2: 10進度数経度をRadian角に変換
> x1 = cos(h1) * cos(t1)      <--コロッセオの p1=(x1,y1,z1)
> y1 = cos(h1) * sin(t1)
> z1 = sin(h1)
> x2 = cos(h2) * cos(t2)      <--度量研究所の p2=(x2,y2,z2)
> y2 = cos(h2) * sin(t2)
> z2 = sin(h2)
> innerpr = x1 * x2 + y1 * y2 + z1 * z2     <-- p1とp2の内積
> angle = acos(innerpr)                     <---p1とp2のなす角度（ラジアン角）. acos は 逆cos関数
> radius = 6378.137           <--地球の半径
> distance = radius * angle
> distance                    <-- p1とp2との2点間の距離
[1] 1112.724

この数値計算の結果から、2点間の距離として 1112.724[km] を得た。我々の計算法もなかなか正確ではないか！実はこれは当たり前で、地図サービスの多くが地球の半径を使って上記の計算（またはそれに近い）方法で距離を求めているからだ (^^;。

演習課題

以下の2地点の緯度経度を精密に調べ、上の計算式をつかって2点間の地球表面に沿った距離を計算せよ。その結果を、Googleマップの距離測定ツールによる結果と比較しなさい。

東京（日本橋）とヨハネスブルグ（タンボ国際空港）
チベット自治区ラサ（ポタラ宮）とローマ（サンピエトロ寺院）
アテネ（パルテノン神殿）とカイロ（大ギザのピラミッド）
ダマスカス（ウマイヤド・モスク）とエルサレム（岩のドーム）
リオデジャネイロ（コルコバードのキリスト像）と東京
ダルフール（Al-Fashir）とコンゴ(Kivu地方、Ntoto）

これに味をしめて、逆のことを考えてみよう。

既知データから地球の大きさを推定する

古来、我々はさまざまな方法で緯度経度の正確な測定技術を進化させてきた。すなわち、それが、航海技術（天測航法）として海上で自身の位置を正確に把握できたのである（直線距離の測定の方が困難をともなう）。その結果、地球の大きさは古くから知られていたのである。素数のふるいで有名なエラトステネス(BC276～196)は、アレクサンドリアとシエネ（アスワン）の緯度差7.2度とその距離925kmから、地球の全周を46,500Kmと計算した（実際は約40,000km）。アレクサンドリアとシエネは実測で843Kmであるので、緯度差7.2度（10進度数）が正しいとすると（実はアスワンはアレクサンドリアの真南ではなく経度も違うのだが、それでも）地球全周は42,150Kmとなって実際の値にかなり近くなる（誤差5%）。

課題

Google Mapを使って、アレクサンドリアとシエネ（アスワン）間の距離を調べなさい。

Gauss先生ほどではない私たちでも、かなりズルをすると地球の大きさ、たとえば地球の半径を測ることができる。正確な距離が分かっている（これは自分で測定するか、または別資料から得る）2点の緯度経度をGoogle Earth/Mapから知って、地球の半径を推定するのである。

地球上の2点$P_1$と$P_2$の2地点間の距離は厳密には地球表面の弧長として測定されるべきなのだが、地球規模に比べて近接していて、2点$P_1$と$P_2$間の地球表面に沿った距離 $R_{12}$ が2点 $P_1$ と $P_2$ 間を結ぶ直線距離 $\tilde{R}_{12}$ と見なし得る場合を考えよう。上記の地球上の2点 $P_1$ と $P_2$ 間の地球表面に沿った距離 $R_{12}$ を求める上の計算結果は、近接2点 $P_1$ と $P_2$ の緯度経度情報と2点間の"直線距離" $\tilde{R}_{12}$ から、地球半径$R_e$を与える式 \[ R_e \simeq \frac{\tilde{R}_{12}}{\cos^{-1} \langle \vec{P_1},\vec{P_2}\rangle} \] と見なすことができる。

課題逆問題 [地球半径の推定]

我々もエラトステネスにならって、2点の緯度経度情報と2点間の直線距離から地球の半径を「推定」してみよう。この場合、先の演習のように、地図サービスで得られる2地点の地球表面に沿った距離データは使ってはいけない。地図サービスから得た値でなく、実測・調査された2点間の直線距離データを使うことが肝要である。地図サービスで得られたデータは、それ自体で地球半径の値を使ってしまっているためだ。ここでは、地球半径の値それ自身を求めたいのである。

厳格にその大きさが（できればミリ単位で）実測・調査された巨大建造物または2地点間の直線距離を探しだし、5組以上リストする。学校の大きさなど管理担当者に尋ねたり設計資料などにあたり、データを収集する。
Google Earth/Mapを使って、その建造物の長さまたは既知の2点$P_1$と$P_2$間の緯度経度を可能な限り精密に取得する。
2地点の単位球面上の直交座標ベクトル $\vec{P_1}=(x_1,y_1,z_1))$ と $\vec{P_2}=(x_2,y_2,z_2)$ から内積をとり、その逆cos関数値から2地点間が地球の中心となす角度[ラジアン]を計算する。
上の式から、地球半径を求める。

さまざまな誤差が伴うため、少なくとも5組程度の建造物または2点間に関する資料について計算すること。