数学基礎力試験結果

数学基礎力試験問題

2015年度数学基礎力測定問題用紙（PDFファイル）: 試験解答と解き方のみ（PDF: 240KB）; 問題解答のための考え方と探求への視線[怒涛編]（PDF: 740KB）

結果速報

348名による試験参加者を得ました。協力していただいた先生方と学生諸君に改めてお礼申し上げます。

採点結果

試験は完全匿名にて実施されました。回収した回答シートをを専用シートリーダにて、20題の設問ごとの5択マーク番号を読み取り、回答基本データとしました（そこからはいかなる個人情報を推測することは不可能です）。

各問の正答にポイント1を、誤答にポイント0を与えて、基本データから回答者ごとに各問の0,1からなる正答/誤答ポイント表を作成、これを試験成績データとしました。受験者ごとの正答ポイントを合計して5倍し、これを受験者の「得点」（100点満点）としました。

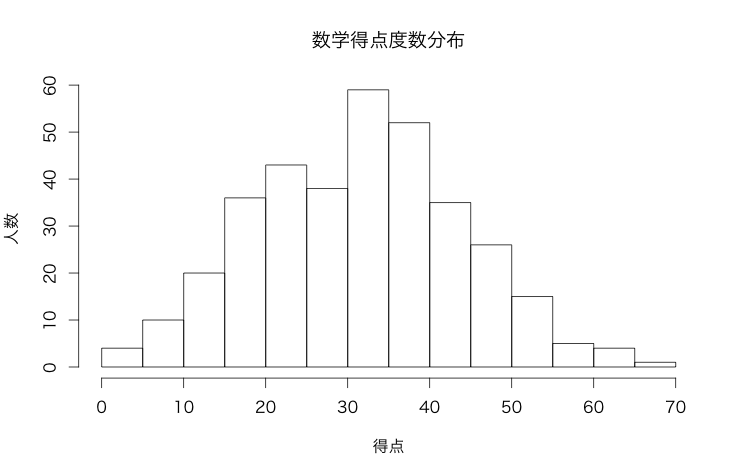
受験者数348名の得点度数分布が以下の図です。 平均点は34.0点でした。

回答傾向

設問20問に特定の偏りがなかったかを調査するために、主成分分析を実施しました。以下、ごく簡単にその結果を報告しておきます。

20問の正答(1)/誤答(0)に関する348人分の試験成績データを主成分分析（全変数を標準化）して得られた20個の固有値を大きなものから降順に並べて固有値の総和（変数の数20に等しい）で除した寄与率の、その累積和は次のようになる（最後の累積値は1になる。

0.1005566 0.1707211 0.2361853 0.2991989 0.3602304
0.4169677 0.4698866 0.5210013 0.5702905 0.6185087
0.6629982 0.7065271 0.7489321 0.7900417 0.8297529
0.8674510 0.9046788 0.9388188 0.9712935 1.0000000

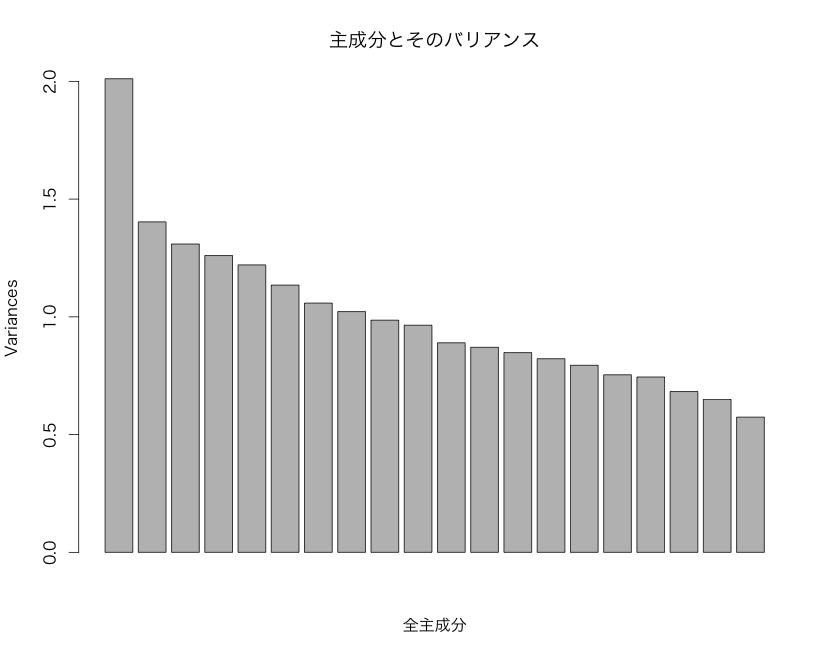
累積寄与率が初めて0.5を越える 0.521 は8番目までの主成分の累積寄与率である。しかし、左図のように全主成分についてのスクリープロットからわかるように、第一主成分以外の固有値の並びにギャップがあるとは言えず、第8成分までの主成分で全体の1/2の情報が要約できるとはいえ、主成分回転楕円体が扁平に偏っているとはいえないことがわかる。回答傾向は格別な傾向を示しているとはいず全体的にばらついており、今回の数学基礎力試験の出題傾向は偏っていたとは言えない（もちろん出題が優れていたわけではない）。